题目内容
18．若-2≤x≤1时，函数f（x）=2ax+a+1的值有正值也有负值，则a的取值范围是（ ）| A． | -$\frac{1}{3}＜a＜\frac{1}{3}$ | B． | a$≤-\frac{1}{3}$ | C． | a$≥\frac{1}{3}$ | D． | 以上都不对 |
分析 利用一次函数的图象是直线，由函数f（x）=2ax+a+1的值有正值也有负值，建立不等式即可求解
解答 解：∵函数f（x）=2ax+a+1的值有正值也有负值，
∴f（-2）和f（1）值的符号相反，
即f（-2）f（1）＜0，
∴（-4a+a+1）（3a+1）＜0，
解得a＞$\frac{1}{3}$或a＜$-\frac{1}{3}$，
所以a的取值范围是a＞$\frac{1}{3}$或a＜$-\frac{1}{3}$；
故选：D
点评 本题主要考查根的存在性对应的应用，关键是由题意建立不等式；属于基础题．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
6．
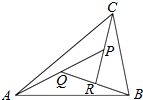如图，在△ABC中，设$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}$=$\overrightarrow b$，AP的中点为Q，BQ的中点为R，CR的中点恰为P，则$\overrightarrow{AP}$等于（ ）
如图，在△ABC中，设$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}$=$\overrightarrow b$，AP的中点为Q，BQ的中点为R，CR的中点恰为P，则$\overrightarrow{AP}$等于（ ）| A． | $\frac{1}{2}（\overrightarrow a+\overrightarrow b）$ | B． | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C． | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D． | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |
3．为了解某班关注NBA是否与性别有关，对该班48人进行了问卷调查得到如下的列联表：
已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为$\frac{2}{3}$
（1）请将右面的表补充完整（不用写计算过程，但要将表格画在答题纸上）；
（2）判断是否有95%的把握认为关注NBA与性别有关？
下面的临界值表，供参考
| 关注NBA | 不关注NBA | 合计 | |
| 男生 | 6 | ||
| 女生 | 10 | ||
| 合计 | 48 |
（1）请将右面的表补充完整（不用写计算过程，但要将表格画在答题纸上）；
（2）判断是否有95%的把握认为关注NBA与性别有关？
下面的临界值表，供参考
| P（K2≥k） | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 60.635 | 7.879 |