题目内容
15.函数y=sin(2x-$\frac{π}{3}$)的单调递减区间是( )| A. | [kπ-$\frac{2π}{3}$,kπ-$\frac{π}{6}$](k∈Z) | B. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) | D. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) |
分析 由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,由此求得x的范围即是函数的单调递减区间.
解答 解:由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,
可得 $kπ+\frac{5}{12}π≤x\;≤kπ+\frac{11}{12}π,k∈Z$,
故函数$y=sin(2x-\frac{π}{3})$的单调递减区间是[kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z),
故选:C.
点评 本题主要考查正弦函数的单调区间的求法,根据正弦函数的单调性建立不等式是解决本题的关键.属于中档题.

练习册系列答案
相关题目
5.以下选项中正确的是( )
| A. | a=7,b=14,A=30°△ABC有两解 | B. | a=9,c=10,A=60°△ABC无解 | ||
| C. | a=6,b=9,A=45°△ABC有两解 | D. | a=30,b=25,A=150°△ABC有一解 |
6.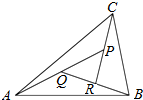 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )| A. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |
3.为了解某班关注NBA是否与性别有关,对该班48人进行了问卷调查得到如下的列联表:
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为$\frac{2}{3}$
(1)请将右面的表补充完整(不用写计算过程,但要将表格画在答题纸上);
(2)判断是否有95%的把握认为关注NBA与性别有关?
下面的临界值表,供参考
| 关注NBA | 不关注NBA | 合计 | |
| 男生 | 6 | ||
| 女生 | 10 | ||
| 合计 | 48 |
(1)请将右面的表补充完整(不用写计算过程,但要将表格画在答题纸上);
(2)判断是否有95%的把握认为关注NBA与性别有关?
下面的临界值表,供参考
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 60.635 | 7.879 |
20.函数f(x)=$\frac{lnx}{x}$(x>0)( )
| A. | 在(0,+∞)上是减函数 | |
| B. | 在(0,+∞)上是减函数 | |
| C. | 在(0,e)上是增函数,在(e,+∞)上是减函数 | |
| D. | 在(0,e)上是减函数,在(e,+∞)上是增函数 |
4.在△ABC中,a=4sin10°,b=sin50°,∠C=70°,则S△ABC=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |