题目内容
16.已知|$\overrightarrow a$|=3,|$\overrightarrow b$|=2,$\overrightarrow a$与$\overrightarrow b$夹角为600,如果(3$\overrightarrow a$+5$\overrightarrow b$)⊥(m$\overrightarrow a$-$\overrightarrow b$),则m值为$\frac{29}{42}$.分析 由(3$\overrightarrow a$+5$\overrightarrow b$)⊥(m$\overrightarrow a$-$\overrightarrow b$),我们易得到(3$\overrightarrow{a}$+5$\overrightarrow{b}$)•(m$\overrightarrow{a}$-$\overrightarrow{b}$)=0,结合|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,我们易得到一个关于m的方程,解方程即可得到答案.
解答 解:∵|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,
∴|$\overrightarrow{a}$|2=9,|$\overrightarrow{b}$|2=4,$\overrightarrow{a}$•$\overrightarrow{b}$=3,
则(3$\overrightarrow{a}$+5$\overrightarrow{b}$)•(m$\overrightarrow{a}$-$\overrightarrow{b}$)
=3m|$\overrightarrow{a}$|2-5|$\overrightarrow{b}$|2+(5m-3)$\overrightarrow{a}$•$\overrightarrow{b}$=27m-20+3(5m-3)
=42m-29,
又∵(3$\overrightarrow{a}$+5$\overrightarrow{b}$)⊥(m$\overrightarrow{a}$-$\overrightarrow{b}$),
∴42m-29=0,
∴m=$\frac{29}{42}$.
故答案为:$\frac{29}{42}$.
点评 本题考查的知识点是平面向量数量积坐标表示的应用,其中根据(3$\overrightarrow a$+5$\overrightarrow b$)⊥(m$\overrightarrow a$-$\overrightarrow b$),得到(3$\overrightarrow{a}$+5$\overrightarrow{b}$)•(m$\overrightarrow{a}$-$\overrightarrow{b}$)=0,进而得到关于m的方程,是解答本类问题的关键.

 灵星计算小达人系列答案
灵星计算小达人系列答案| A. | 7 | B. | 9 | C. | 11 | D. | 15 |
| A. | a=7,b=14,A=30°△ABC有两解 | B. | a=9,c=10,A=60°△ABC无解 | ||
| C. | a=6,b=9,A=45°△ABC有两解 | D. | a=30,b=25,A=150°△ABC有一解 |
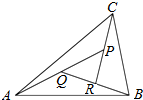 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )| A. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |
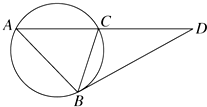 过D作圆的切线切于B点,作割线交圆于A、C两点,若BD=3,AD=4,AB=2,则BC=$\frac{3}{2}$.
过D作圆的切线切于B点,作割线交圆于A、C两点,若BD=3,AD=4,AB=2,则BC=$\frac{3}{2}$.