题目内容
1．
如图，将全体正奇数排成一个三角形数阵：按照以上排列的规律，第45行从左向右的第17个数为2013．
分析 由三角形数阵，知第n行的前面共有1+2+3+…+（n-1）个连续奇数，再由等差数列的前n项和公式化简，再由奇数的特点求出第n行从左向右的第m个数，代入可得答案．
解答 解：观察三角形数阵，
知第n行前共有1+2+3+…+（n-1）=$\frac{n（n-1）}{2}$个奇数，
第n行从左向右的第m个数为2[$\frac{n（n-1）}{2}$+m]-1=n2-n+2m-1，
当n=45，m=17时，第45行从左向右的第17个数为：452-45+2×17-1=2013，
故答案为：2013
点评 本题考查了归纳推理在数阵的排列规律的应用，以及等差数列的前n项和公式应用，关键是发现规律并应用所学知识，来解答问题．
练习册系列答案
相关题目
6．
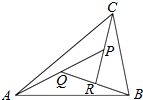如图，在△ABC中，设$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}$=$\overrightarrow b$，AP的中点为Q，BQ的中点为R，CR的中点恰为P，则$\overrightarrow{AP}$等于（ ）
如图，在△ABC中，设$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}$=$\overrightarrow b$，AP的中点为Q，BQ的中点为R，CR的中点恰为P，则$\overrightarrow{AP}$等于（ ）| A． | $\frac{1}{2}（\overrightarrow a+\overrightarrow b）$ | B． | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C． | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D． | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |