题目内容
16.用适当方法证明下列不等式:(Ⅰ)用综合法证明:若a>0,b>0,求证:(a+b)($\frac{1}{a}+\frac{1}{b}$)≥4;
(Ⅱ)用分析法证明:$\sqrt{6}+\sqrt{7}>2\sqrt{2}+\sqrt{5}$.
分析 (Ⅰ)利用基本不等式,再相乘,即得所证.
(Ⅱ)寻找使$\sqrt{6}+\sqrt{7}>2\sqrt{2}+\sqrt{5}$成立的充分条件,直到使不等式成立的条件显然具备为止.
解答 证明:(Ⅰ)∵$a>0,b>0∴a+b≥2\sqrt{ab}$,…(2分)
∴$\frac{1}{a}+\frac{1}{b}≥2\sqrt{\frac{1}{ab}}$,…(4分)
∴(a+b)($\frac{1}{a}+\frac{1}{b}$)≥4.…(6分)
(Ⅱ)要证$\sqrt{6}+\sqrt{7}>2\sqrt{2}+\sqrt{5}$.成立
只需证${({\sqrt{6}+\sqrt{7}})^2}>{({2\sqrt{2}+\sqrt{5}})^2}$,…(8分)
即证$13+2\sqrt{42}>13+4\sqrt{10}$,
只需证$\sqrt{42}>2\sqrt{10}$,
即证42>40显然为真,
故原式成立.…(12分)
点评 本题主要考查用综合法和分析法证明不等式,体现了转化的数学思想,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.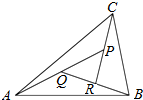 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )| A. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |
4.在△ABC中,a=4sin10°,b=sin50°,∠C=70°,则S△ABC=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |