题目内容
已知函数 .
.
(1)若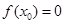 ,求
,求 的值;
的值;
(2)求函数 的单调递增区间.
的单调递增区间.
(1)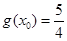 ;(2)
;(2)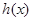 的单调递增区间是
的单调递增区间是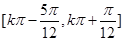 .
.
解析试题分析:本题考查两角和与差的正弦公式、降幂公式以及运用三角公式进行三角变换求三角函数的单调区间.第一问,用降幂公式化简式子,得到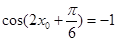 解出
解出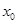 ,再代入到
,再代入到 中用诱导公式化简;第二问,先利用降幂公式、两角和与差的正弦公式化简
中用诱导公式化简;第二问,先利用降幂公式、两角和与差的正弦公式化简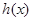 表达式,再数形结合求单调区间.
表达式,再数形结合求单调区间.
试题解析:(1)由题设知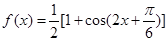 .
.
因为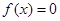 ,所以
,所以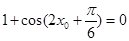 ,
, 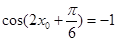 ,即
,即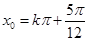 (
(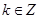 ).
).
所以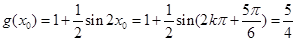 . (6分)
. (6分)
(2) 
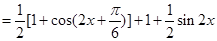
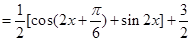
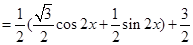
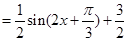
当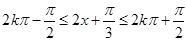 ,即
,即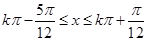 (
(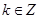 )时,
)时,
函数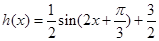 是增函数,
是增函数,
故函数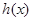 的单调递增区间是
的单调递增区间是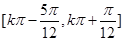 (
(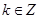 ).(12分)
).(12分)
考点:1.降幂公式;2.诱导公式;3.两角和与差的正弦公式;4.三角函数的单调性.

练习册系列答案
相关题目
 中,
中, 的对边分别为
的对边分别为 且
且 成等差数列.
成等差数列. 的范围.
的范围.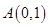 ,
,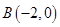 ,
, ,
, 为坐标原点,向量
为坐标原点,向量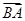 与向量
与向量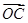 共线.
共线.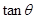 的值;
的值;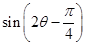 的值.
的值.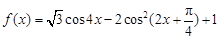 .
.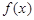 的最小正周期;
的最小正周期;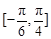 上的取值范围.
上的取值范围.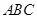 中,角
中,角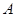 、
、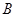 、
、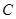 所对的边分别为
所对的边分别为 、
、 、
、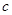 ,且
,且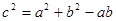 .
. ,求角
,求角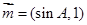 ,
,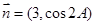 ,试求
,试求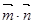 的最大值.
的最大值. .
. 的最小正周期和最大值;
的最小正周期和最大值; 为锐角,且
为锐角,且 ,求
,求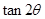 的值.
的值.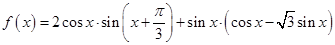
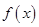 的最小正周期和单调递减区间;(6分);
的最小正周期和单调递减区间;(6分);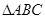 中,
中,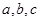 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若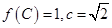 ,求
,求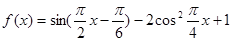 ,函数
,函数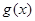 与函数
与函数 图像关于
图像关于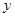 轴对称.
轴对称.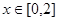 时,求
时,求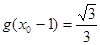 ,
,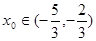 求
求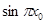 值.
值.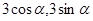 )
)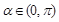 ,且
,且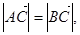 ,求
,求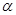 的大小;
的大小;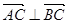 ,求
,求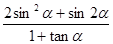 的值.
的值.