题目内容
在△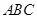 中,角
中,角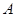 、
、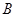 、
、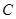 所对的边分别为
所对的边分别为 、
、 、
、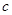 ,且
,且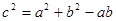 .
.
(Ⅰ)若 ,求角
,求角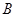 ;
;
(Ⅱ)设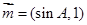 ,
,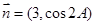 ,试求
,试求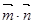 的最大值.
的最大值.
(Ⅰ)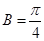 ;(Ⅱ)
;(Ⅱ)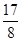 .
.
解析试题分析:(Ⅰ)由则可联想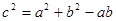 余弦定理求出角
余弦定理求出角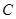 ,而由
,而由 ,则易联想两角差的正切公式,求得
,则易联想两角差的正切公式,求得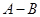 ,结合三角形内角和定理可求出角
,结合三角形内角和定理可求出角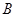 ;(Ⅱ)很显然
;(Ⅱ)很显然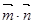 是角
是角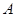 的三角函数,由角
的三角函数,由角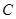 的大小则可确定角
的大小则可确定角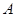 的取值范围,于是问题就转化为三角函数的值域问题,一般可化为
的取值范围,于是问题就转化为三角函数的值域问题,一般可化为 的类型后解决,也可能化为一个三角函数的二次型问题解决.
的类型后解决,也可能化为一个三角函数的二次型问题解决.
试题解析:∵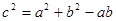 ;∴
;∴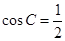 ,∵
,∵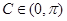 ∴
∴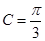
(1)∵
∴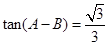 ∵
∵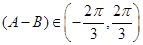
∴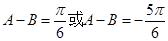 ,又
,又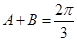
∴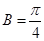 或
或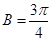 (舍去)∴
(舍去)∴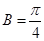 7分
7分
(2)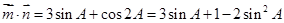 令
令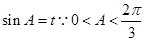 ∴
∴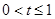
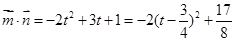 ∴
∴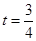 时,
时,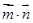 的最大值为
的最大值为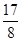 14分
14分
考点:余弦定理、两角差的正切公式、正弦函数的性质.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
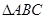 中
中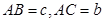 ,
, 为线段
为线段 上一点,且
上一点,且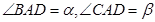 ,线段
,线段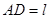 .
.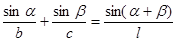 ;
;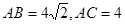 ,
,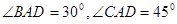 ,试求线段
,试求线段 的长.
的长. 中,角
中,角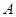 ,
,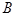 ,
,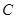 所对的边分别为
所对的边分别为 ,
,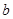 ,
,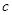 ,且
,且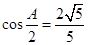 .
.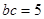 ,求
,求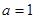 ,求
,求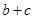 的最大值.
的最大值. 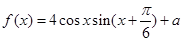 的最大值为2.
的最大值为2.
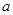 的值及
的值及 的最小正周期;
的最小正周期;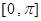 上的图像.
上的图像.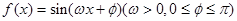 为偶函数,周期为2
为偶函数,周期为2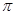 .
.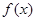 的解析式;
的解析式;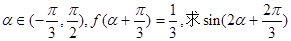 的值.
的值. .
.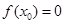 ,求
,求 的值;
的值; 的单调递增区间.
的单调递增区间.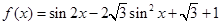 .
. 的最小正周期;
的最小正周期;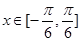 时,求
时,求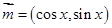 和
和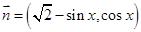 ,
,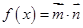 ,写出函数
,写出函数 的最小正周期;并求函数
的最小正周期;并求函数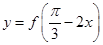 的单调区间;
的单调区间;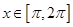 ,求
,求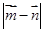 的最大值.
的最大值.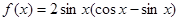 ,其中
,其中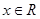
 的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数
的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数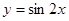 的图像变成
的图像变成 的图像;(要求变换的先后顺序)
的图像;(要求变换的先后顺序)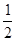 倍,
倍,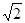 倍,
倍,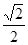 倍,
倍,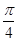 个单位,
个单位,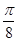 个单位,
个单位,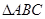 中角
中角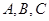 对应边分别为
对应边分别为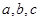 ,
,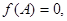
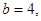
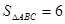 ,求
,求 的长.
的长.