题目内容
已知平面直角坐标系上的三点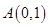 ,
,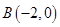 ,
, ,
, 为坐标原点,向量
为坐标原点,向量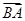 与向量
与向量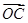 共线.
共线.
(1)求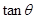 的值;
的值;
(2)求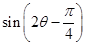 的值.
的值.
(1)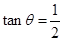 ;(2)
;(2) .
.
解析试题分析:(1)法一是利用两平面向量共线的基本定理得到坐标之间的关系,进而利用弦化切的方法求出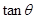 的值;法二是利用平面向量共线的基本定理结合坐标运算得到向量
的值;法二是利用平面向量共线的基本定理结合坐标运算得到向量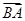 与
与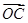 的坐标之间的关系,然后利用除法求出
的坐标之间的关系,然后利用除法求出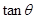 的值;(2)利用(1)中
的值;(2)利用(1)中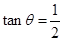 以及同角三角函数中的商数关系和平方关系并结合角
以及同角三角函数中的商数关系和平方关系并结合角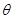 的范围列方程组求出
的范围列方程组求出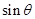 和
和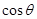 的值,进而求出
的值,进而求出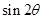 和
和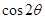 的值,最终再利用两角差的正弦公式求出
的值,最终再利用两角差的正弦公式求出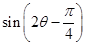 的值.
的值.
试题解析:法1:由题意得: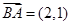 ,
,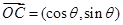 , 2分
, 2分
∵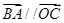 ,∴
,∴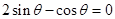 ,∴
,∴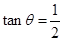 . 5分
. 5分
法2:由题意得: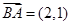 ,
,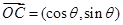 , 2分
, 2分
∵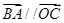 ,∴
,∴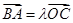 ,∴
,∴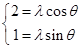 ,∴
,∴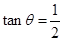 . 5分
. 5分
(2)∵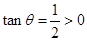 ,
,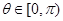 ,∴
,∴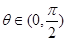 , 6分
, 6分
由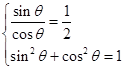 ,解得
,解得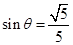 ,
, , 8分
, 8分
∴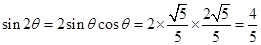 ; 9分
; 9分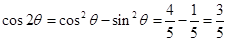 ; 10分
; 10分
∴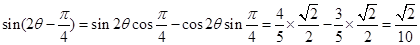 . 12分
. 12分
考点:1.平面向量的坐标运算;2.同角三角函数的基本关系;3.二倍角;4.两角差的正弦公式

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
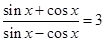
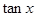 的值;
的值; 是第三象限的角,化简三角式
是第三象限的角,化简三角式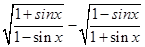 ,并求值.
,并求值.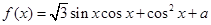 .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;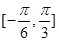 上的最大值与最小值的和为
上的最大值与最小值的和为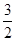 ,求
,求 的值.
的值.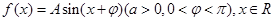 的最大值是1,其图像经过点
的最大值是1,其图像经过点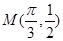 。
。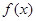 的解析式;
的解析式; ,且
,且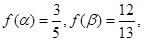 求
求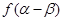 的值.
的值. 中,角
中,角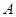 ,
,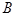 ,
,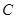 所对的边分别为
所对的边分别为 ,
,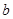 ,
,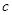 ,且
,且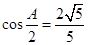 .
.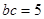 ,求
,求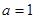 ,求
,求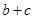 的最大值.
的最大值.  ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
 ,求
,求 面积的最大值及此时
面积的最大值及此时 的值.
的值.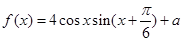 的最大值为2.
的最大值为2.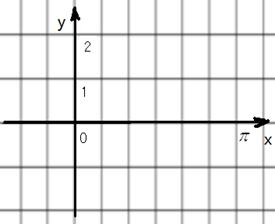
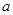 的值及
的值及 的最小正周期;
的最小正周期;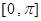 上的图像.
上的图像. .
.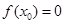 ,求
,求 的值;
的值; 的单调递增区间.
的单调递增区间.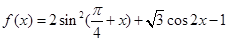 .
.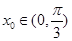 ,使f(x0)=1,求x0的值;
,使f(x0)=1,求x0的值;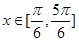 ,条件q:
,条件q: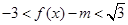 ,若p是q的充分条件,求实数m的取值范围.
,若p是q的充分条件,求实数m的取值范围.