题目内容
已知函数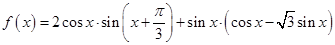
(1)求函数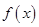 的最小正周期和单调递减区间;(6分);
的最小正周期和单调递减区间;(6分);
(2)在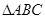 中,
中,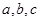 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若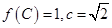 ,求
,求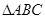 面积的最大值.(6分)
面积的最大值.(6分)
(1)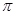 ,
,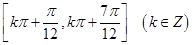 ;(2)
;(2)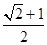
解析试题分析:(1)一般的,求三角函数的最值、周期、单调区间、对称性等性质问题,都要将三角函数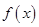 化为
化为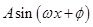 形式,再求解;(2)由
形式,再求解;(2)由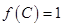 利用三角函数求性质出角C,再利用余弦定理结合基本不等式,求出ab的最大值,代入面积公式可得.
利用三角函数求性质出角C,再利用余弦定理结合基本不等式,求出ab的最大值,代入面积公式可得.
试题解析:(1)函数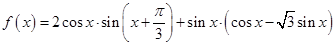
=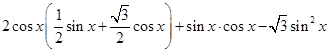
= =
=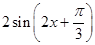
所以函数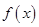 的最小正周期为
的最小正周期为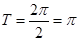 ,
,
由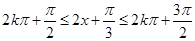 得
得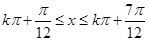 ,
,
即单调递减区间为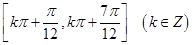 ;(6分)
;(6分)
(2)由 得
得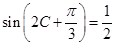 ,
,
由于C是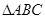 的内角,所以
的内角,所以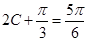 ,故
,故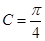 ,
,
由余弦定理得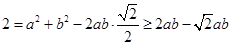 ,
,
所以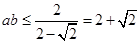 (当且仅当
(当且仅当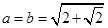 时取等号)
时取等号)
所以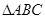 面积的最大值为,
面积的最大值为,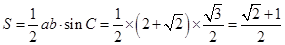 . (12分)
. (12分)
考点:1、三角函数及求值;2、余弦定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
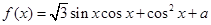 .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;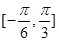 上的最大值与最小值的和为
上的最大值与最小值的和为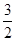 ,求
,求 的值.
的值.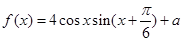 的最大值为2.
的最大值为2.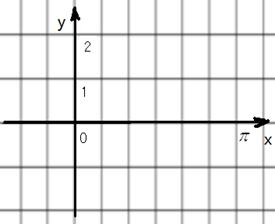
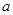 的值及
的值及 的最小正周期;
的最小正周期;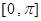 上的图像.
上的图像. .
.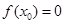 ,求
,求 的值;
的值; 的单调递增区间.
的单调递增区间.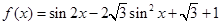 .
. 的最小正周期;
的最小正周期;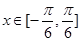 时,求
时,求 ,其中,角
,其中,角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点 ,且
,且 .
. 点的坐标为(-
点的坐标为(- ),求
),求 的值;
的值; 上的一个动点,试确定角
上的一个动点,试确定角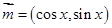 和
和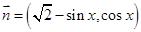 ,
,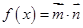 ,写出函数
,写出函数 的最小正周期;并求函数
的最小正周期;并求函数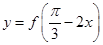 的单调区间;
的单调区间;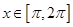 ,求
,求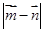 的最大值.
的最大值.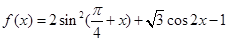 .
.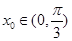 ,使f(x0)=1,求x0的值;
,使f(x0)=1,求x0的值;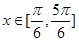 ,条件q:
,条件q: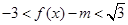 ,若p是q的充分条件,求实数m的取值范围.
,若p是q的充分条件,求实数m的取值范围.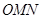 是半径为2,圆心角为
是半径为2,圆心角为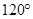 的扇形,
的扇形,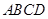 是扇形的内接矩形.
是扇形的内接矩形.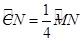 时,求
时,求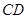 的长;
的长;