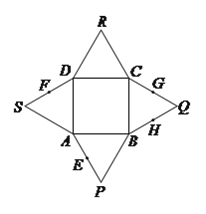
题目内容
【题目】已知圆C的圆心在直线3x+y﹣1=0上,且圆C在x轴、y轴上截得的弦长AB和MN分别为 ![]() 和
和 ![]() .
.
(1)求圆C的方程;
(2)若圆心C位于第四象限,点P(x,y)是圆C内一动点,且x,y满足 ![]() ,求
,求 ![]() 的范围.
的范围.
【答案】
(1)解:设圆心为(a,b),半径为r,
则有 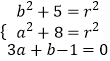
得 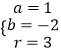 或
或  ,
,
圆C:(x﹣1)2+(y+2)2=9或 ![]()
(2)解:∵圆心C在第四象限,∴圆C的方程为(x﹣1)2+(y+2)2=9,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∵x,y满足 ![]() ,
,
∴ ![]() (或
(或 ![]() ),
),
又∵P在圆C内,满足(x﹣1)2+(y+2)2<9且 ![]()
∴4y2+8y﹣5<0,解得 ![]() ,
,
∴ ![]() .
.
∴ ![]() 的范围[﹣
的范围[﹣ ![]() ,10)
,10)
【解析】(1)设出圆的圆心与半径,根据题意列出方程组,解方程组即可求得圆的方程;(2)根据圆心的象限位置确定圆的具体方程及点A,B的具体坐标,然后用x,y表示出![]() ,再结合x,y的关系与点P在圆C内求得其取值范围.
,再结合x,y的关系与点P在圆C内求得其取值范围.
【考点精析】通过灵活运用直线与圆的三种位置关系,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点即可以解答此题.

练习册系列答案
相关题目