题目内容
【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() 和直线
和直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,并且被圆
,并且被圆![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的方程.
的方程.
【答案】(1)(x-1)2+(y+2)2=2;(2)x=2或3x-4y-6=0.
【解析】试题分析:(1)先求线段AB的垂直平分线方程为![]() ,设圆心的坐标为C(a,-a-1),由圆心到点的距离和到切线的距离相等求解即可;
,设圆心的坐标为C(a,-a-1),由圆心到点的距离和到切线的距离相等求解即可;
(2)由题知圆心C到直线l的距离![]() ,进而讨论直线斜率存在不存在两种情况求解即可.
,进而讨论直线斜率存在不存在两种情况求解即可.
试题解析:
(1)由题知,线段AB的中点M(1,-2), ![]() ,
,
线段AB的垂直平分线方程为![]() ,即
,即![]() ,
,
设圆心的坐标为C(a,-a-1),
则![]() ,
,
化简,得a2-2a+1=0,解得a=1.∴C(1,-2),
半径r=|AC|=![]() =
=![]() .
.
∴圆C的方程为(x-1)2+(y+2)2=2.
(解二:可设原方程用待定系数法求解)
(2)由题知圆心C到直线l的距离![]() ,
,
①当直线l的斜率不存在时,直线l的方程为x=2,此时直线l被圆C截得的弦长为2,
满足条件.
②当直线l的斜率存在时,设直线l的方程为![]() ,由题意得
,由题意得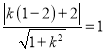 ,
,
解得k=![]() ,
,
∴直线l的方程为y=![]() (x-2).
(x-2).
综上所述,直线l的方程为x=2或3x-4y-6=0.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目