题目内容
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且（a﹣c）（sinA+sinC）=（a﹣b）sinB．
（1）求角C的大小；
（2）若c= 
≤a，求2a﹣b的取值范围．
【答案】
（1）解：由已知和正弦定理得：（a﹣c）（a+c）=b（a﹣b）
故a2﹣c2=ab﹣b2，故a2+b2﹣c2=ab，
得 
，所以 
（2）解：因为 
，
由正弦定理，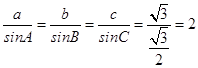 
得a=2sinA，b=2sinB，
= 
因为c≤a，所以 
，
所以 
【解析】（1）利用正弦定理以及余弦定理，转化求解即可．（2）利用正弦定理化简2a﹣b的表达式，通过两角和与差的三角函数化简，结合角的范围求解最值即可．
【考点精析】利用正弦定理的定义对题目进行判断即可得到答案，需要熟知正弦定理:
．
练习册系列答案
相关题目
【题目】在某城市气象部门的数据中，随机抽取了100天的空气质量指数的监测数据如表：
空气质量指数t | （0，50] | （50，100] | （100，150] | （150，200] | （200，300] | （300，+∞） |
质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
天数K | 5 | 23 | 22 | 25 | 15 | 10 |
（1）在该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量t（t取整数）存在如下关系y= 
，且当t＞300时，y＞500估计在某一医院收治此类病症人数超过200人的概率；
（2）若在（1）中，当t＞300时，y与t的关系拟合于曲线 
，现已取出了10对样本数据（ti ， yi）（i=1，2，3，…，10），且 
=42500， 
=500，求拟合曲线方程． （附：线性回归方程 
=a+bx中，b= 
，a= ﹣b 
）
