题目内容
(本题满分14分)已知点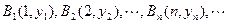 (
(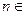 N
N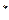 )顺次为直线
)顺次为直线 上的点,点
上的点,点
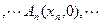 (
(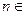 N
N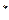 )顺次为
)顺次为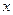 轴上的点,其中
轴上的点,其中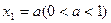 ,对任意的
,对任意的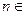 N
N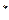 ,点
,点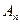 、
、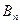 、
、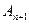 构成以
构成以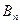 为顶点的等腰三角形.(Ⅰ)证明:数列
为顶点的等腰三角形.(Ⅰ)证明:数列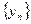 是等差数列;(Ⅱ)求证:对任意的
是等差数列;(Ⅱ)求证:对任意的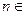 N
N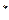 ,
,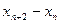 是常数,并求数列
是常数,并求数列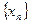 的通项公式; (Ⅲ)在上述等腰三角形
的通项公式; (Ⅲ)在上述等腰三角形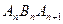 中是否存在直角三角形,若存在,求出此时
中是否存在直角三角形,若存在,求出此时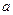 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
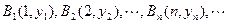 (
(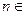 N
N )顺次为直线
)顺次为直线 上的点,点
上的点,点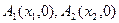
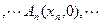 (
(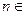 N
N )顺次为
)顺次为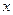 轴上的点,其中
轴上的点,其中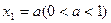 ,对任意的
,对任意的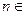 N
N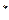 ,点
,点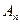 、
、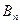 、
、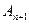 构成以
构成以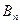 为顶点的等腰三角形.(Ⅰ)证明:数列
为顶点的等腰三角形.(Ⅰ)证明:数列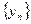 是等差数列;(Ⅱ)求证:对任意的
是等差数列;(Ⅱ)求证:对任意的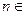 N
N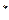 ,
,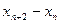 是常数,并求数列
是常数,并求数列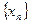 的通项公式; (Ⅲ)在上述等腰三角形
的通项公式; (Ⅲ)在上述等腰三角形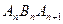 中是否存在直角三角形,若存在,求出此时
中是否存在直角三角形,若存在,求出此时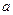 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1) (2)
(2)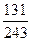
 (2)
(2)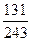
解: (Ⅰ)依题意有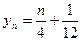 ,于是
,于是 .所以数列
.所以数列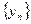 是等差数列.….2分
是等差数列.….2分
(Ⅱ)由题意得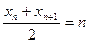 ,即
,即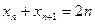 , (
, (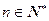 ) ①
) ①
所以又有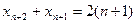 . ②…4分由②
. ②…4分由② ①得
①得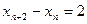 ,
,
可知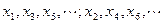 都是等差数列.那么得
都是等差数列.那么得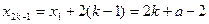 ,
,
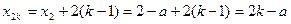 . (
. (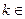

 故
故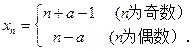
(Ⅲ)当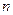 为奇数时,
为奇数时,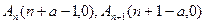 ,所以
,所以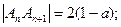
当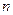 为偶数时,
为偶数时,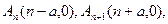 所以
所以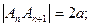 作
作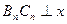 轴,垂足为
轴,垂足为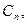 则
则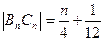 ,要使等腰三角形
,要使等腰三角形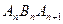 为直角三角形,必须且只需
为直角三角形,必须且只需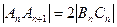 . 当
. 当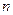 为奇数时,有
为奇数时,有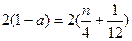 ,即
,即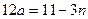 ①当
①当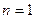 时,
时,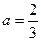 ;当
;当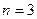 时,
时,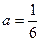 ;当
;当 , ①式无解.当
, ①式无解.当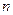 为偶数时,有
为偶数时,有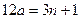 ,同理可求得
,同理可求得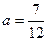 . 综上所述,上述等腰三角形
. 综上所述,上述等腰三角形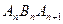 中存在直角三角形,此时
中存在直角三角形,此时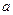 的值为
的值为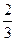 或
或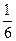 或
或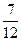 ...14分
...14分
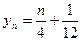 ,于是
,于是 .所以数列
.所以数列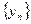 是等差数列.….2分
是等差数列.….2分(Ⅱ)由题意得
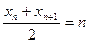 ,即
,即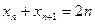 , (
, (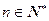 ) ①
) ①所以又有
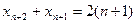 . ②…4分由②
. ②…4分由②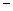 ①得
①得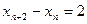 ,
,可知
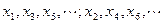 都是等差数列.那么得
都是等差数列.那么得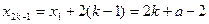 ,
,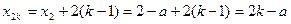 . (
. (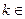

 故
故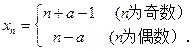
(Ⅲ)当
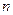 为奇数时,
为奇数时,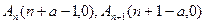 ,所以
,所以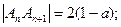
当
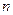 为偶数时,
为偶数时,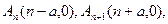 所以
所以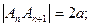 作
作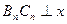 轴,垂足为
轴,垂足为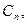 则
则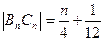 ,要使等腰三角形
,要使等腰三角形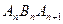 为直角三角形,必须且只需
为直角三角形,必须且只需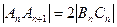 . 当
. 当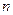 为奇数时,有
为奇数时,有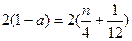 ,即
,即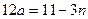 ①当
①当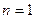 时,
时,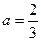 ;当
;当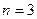 时,
时,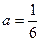 ;当
;当 , ①式无解.当
, ①式无解.当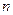 为偶数时,有
为偶数时,有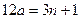 ,同理可求得
,同理可求得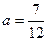 . 综上所述,上述等腰三角形
. 综上所述,上述等腰三角形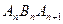 中存在直角三角形,此时
中存在直角三角形,此时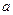 的值为
的值为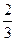 或
或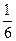 或
或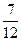 ...14分
...14分
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
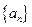 的前
的前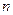 项和为
项和为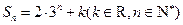
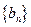 满足
满足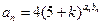 ,
, 为数列
为数列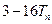 与
与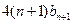 的大小,并证明你的结论.
的大小,并证明你的结论.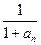 ,求a2008。
,求a2008。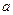 吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出
吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出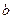 吨,设
吨,设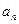 为正式运营后第
为正式运营后第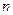 年年底的石油储量.(Ⅰ)求
年年底的石油储量.(Ⅰ)求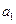 、
、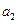 、
、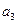 ; (Ⅱ)猜测出
; (Ⅱ)猜测出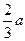 吨,如果
吨,如果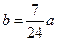 吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:
吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据: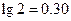 ,
,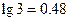 )
)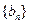 的前
的前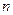 项和为
项和为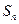 ,且
,且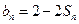 ;数列
;数列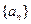 为等差数列,且
为等差数列,且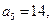
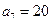 .
.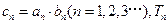 为数列
为数列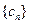 的前
的前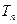 .
.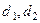 为公差的等差数列
为公差的等差数列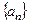 ,
,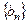 ,满足
,满足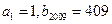 .(Ⅰ)若
.(Ⅰ)若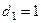 ,且存在正整数
,且存在正整数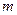 ,使得
,使得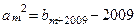 ,求
,求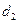 的最小值;(Ⅱ)若
的最小值;(Ⅱ)若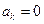 ,
,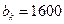 且数列
且数列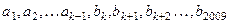 ,的前项
,的前项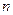 和
和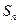 满足
满足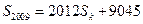 ,求
,求 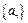 中,若a1 + a2 + a3 + a4 + a5 = 20,则a3 = ( )
中,若a1 + a2 + a3 + a4 + a5 = 20,则a3 = ( )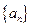 满足
满足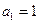 ,
,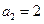 ,
,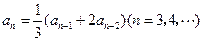 .数列
.数列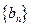 满足
满足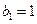 ,
,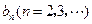 是非零整数,且对任意的正整数
是非零整数,且对任意的正整数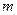 和自然数
和自然数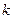 ,都有
,都有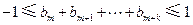 .
.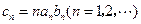 ,求数列
,求数列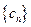 的前
的前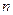 项和
项和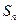 .
.