Question

【题目】集合A是由满足以下性质的函数f（x）组成的：对于任意x≥0，f（x） ∈[-2，4]且f（x）在[0，+∞）上是增函数.

（Ⅰ）试判断与（x≥0）是否属于集合A，并说明理由；

（Ⅱ）对于（Ⅰ）中你认为属于集合A的函数f（x），证明：对于任意的x≥0，都有f（x）+f（x+2）<2f（x+1）.

Answer 1

【答案】(1) ， (2)见解析.

【解析】试题分析：（I）由已知可得函数的值域，从而可得，对于，只要分别判断函数定义域是否满足条件①，值域是否满足条件②，单调性是否满足条件③，即可得答案；（II）由（I）知， 属于集合，原不等式为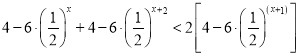，利用作差法指数幂的运算法则化简整理可以证明结论.

试题解析：（Ⅰ） ， ，理由如下：

由于（49）=5>4， （49） [-2，4]，所以（x）A.

对于

因为在[0，+∞）上是减函数，且其值域为（0，1]，

所以在区间[0，+∞）上是增函数.

所以≥f（0）=-2，且=<4，

所以对于任意x≥0，f（x）∈[-2，4].

所以∈A

（Ⅱ）由（Ⅰ）得： ，

f（x+1）=4-=4-3·，

所以2f（x+1）-[f（x）+f（x+2）]=2[4-3·]-[4-6·+4-·]=·>0，

所以对于任意的x≥0，都有f（x）+f（x+2）<2f（x+1）.