题目内容
16.已知函数f(x)=2$\sqrt{3}$sin(3ωx+$\frac{π}{3}$),ω>0.(1)若f(x)在(0,$\frac{π}{3}$)上单调递增,求ω的最大值;
(2)若f(x+θ),θ∈(0,π)是周期为2π的偶函数,求ω及θ的值.
分析 (1)由函数的解析式利用正弦函数的单调增区间,求得函数的增区间为[$\frac{2kπ-\frac{5π}{6}}{3ω}$,$\frac{2kπ+\frac{π}{6}}{3ω}$],依题意知,(0,$\frac{π}{3}$)⊆[-$\frac{5π}{18ω}$,$\frac{π}{18ω}$],可得$\frac{π}{3}$≤$\frac{π}{18ω}$,由此求得ω的最大值.
(2)根据函数f(x+θ)=2$\sqrt{3}$sin(3ωx+3ωθ+$\frac{π}{3}$),此函数的周期T=$\frac{2π}{3ω}$=2π,求得ω 的值,再根据 f(x+θ)为偶函数,可得sin(θ+$\frac{π}{3}$)=±1,故θ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,再结合θ∈(0,π),求得θ 的值.
解答 解:(1)对于函数f(x)=2$\sqrt{3}$sin(3ωx+$\frac{π}{3}$),ω>0,令2kπ-$\frac{π}{2}$≤3ωx+$\frac{π}{3}$≤2kπ-$\frac{π}{2}$,k∈z,
求得$\frac{2kπ-\frac{5π}{6}}{3ω}$≤x≤$\frac{2kπ+\frac{π}{6}}{3ω}$,可得函数的增区间为[$\frac{2kπ-\frac{5π}{6}}{3ω}$,$\frac{2kπ+\frac{π}{6}}{3ω}$],
依题意知,当k=0时,(0,$\frac{π}{3}$)⊆[-$\frac{5π}{18ω}$,$\frac{π}{18ω}$],∴$\frac{π}{3}$≤$\frac{π}{18ω}$,∴ω≤$\frac{1}{6}$,
即ω的最大值为$\frac{1}{6}$.
(2)函数f(x+θ)=2$\sqrt{3}$sin[3ω(x+θ)+$\frac{π}{3}$]=2$\sqrt{3}$sin(3ωx+3ωθ+$\frac{π}{3}$),故函数的周期T=$\frac{2π}{3ω}$=2π,
求得ω=$\frac{1}{3}$,∴f(x+θ)=2$\sqrt{3}$sin(x+θ+$\frac{π}{3}$),为偶函数,
∴当x=0时,sin(θ+$\frac{π}{3}$)=±1,∴θ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,即θ=kπ+$\frac{π}{6}$,k∈z.
再结合θ∈(0,π),可得θ=$\frac{π}{6}$.
点评 本题主要考查正弦函数的单调性、周期性和奇偶性,根据三角函数的值求角,属于基础题.

| A. | $\frac{12}{ln2}$ | B. | $\frac{20}{ln2}$ | C. | $\frac{18}{ln2}$ | D. | $\frac{16}{ln2}$ |
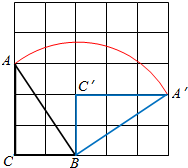 如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.
如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.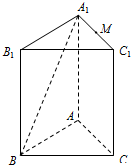 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.