题目内容
7．如图，已知⊙O1与⊙O2外切于点A，⊙O1的弦BC的延长线切⊙O2于点D，BA交⊙O2于点E，求证：∠CAD=∠DAE．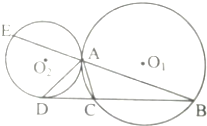
分析 过点A作两圆的公切线GF交BD于G，延长DA交⊙O1于H，连接BH，根据已知条件和图形证明△AED∽△ADC，得到答案
解答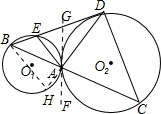 
证明：过点A作两圆的公切线GF交BD于G，延长DA交⊙O1于H，连接BH，
则∠ADC=∠FAC，∠H=∠BAG，
∵∠BAG=∠FAC，
∴∠H=∠ADC，
根据圆内接四边形的性质可知：∠H=∠DEA，
∴∠DEA=∠ADC，
又∵AE：AD=ED：DC，
∴△AED∽△ADC，
∴∠CAD=∠DAE．
点评 本题考查相切两圆的性质和相似三角形的判定和性质，正确作出辅助线构造相似三角形是解题的关键，注意两圆公切线的性质的应用．
练习册系列答案
相关题目
17．山东某市2008年至2012年新建商品住宅每平方米的均价y
（单位：千元）的数据如表：
（Ⅰ）求y关于x的线性回归方程$\hat y=\hat b•x+\hat a$；
（Ⅱ）利用（Ⅰ）中的回归方程，分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况，并预测该市2015年新建商品住宅每平方米的均价．
附：回归直线的斜率和截距的最小二乘估计公式分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x•\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$，$\hat a=\bar y-\hat b•\bar x$．
（单位：千元）的数据如表：
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 每平米均价y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
（Ⅱ）利用（Ⅰ）中的回归方程，分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况，并预测该市2015年新建商品住宅每平方米的均价．
附：回归直线的斜率和截距的最小二乘估计公式分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x•\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$，$\hat a=\bar y-\hat b•\bar x$．
12．确定结论“X与Y有关系”的可信度为99.5%时，则随即变量k2的观测值k必须（ ）
| A． | 大于10.828 | B． | 大于7.879 | C． | 小于6.635 | D． | 大于2.706 |