题目内容
如图,在矩形ABCD中,AB=2,AD=1,E为CD的中点,将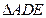 沿AE折起,使平面
沿AE折起,使平面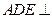 平面ABCE,得到几何体
平面ABCE,得到几何体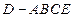 .(1)求证:
.(1)求证: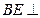 平面
平面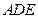 ;(2)求BD和平面
;(2)求BD和平面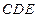 所成的角的正弦值.
所成的角的正弦值.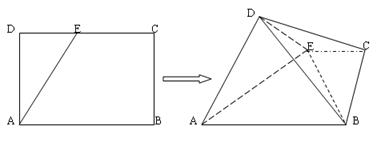
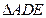 沿AE折起,使平面
沿AE折起,使平面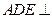 平面ABCE,得到几何体
平面ABCE,得到几何体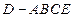 .(1)求证:
.(1)求证: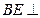 平面
平面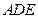 ;(2)求BD和平面
;(2)求BD和平面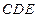 所成的角的正弦值.
所成的角的正弦值.
(1)略(2)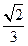
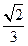
证明:(1)过D作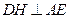 于H.由平面
于H.由平面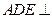 平面
平面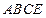 得,
得,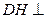 平面
平面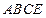 ,所以
,所以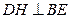 ,由题意可得
,由题意可得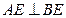 ,因此
,因此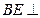 平面
平面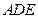 ..
..
(2)在平面CDE内,过C作CE的垂线,与过D作CE的平行线交于F,再过B作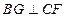 于G,连结DG,CH,BH可得
于G,连结DG,CH,BH可得 平面
平面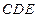 ;所以
;所以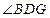 为BD和平面CDE所成的角.在
为BD和平面CDE所成的角.在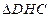 中,
中, 中,可得
中,可得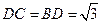 ,又
,又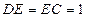 ,因此
,因此
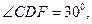
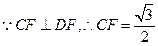 .由题意得
.由题意得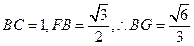 ,因此
,因此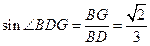 ,BD和平面
,BD和平面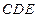 所成的角的正弦值为
所成的角的正弦值为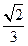 .
.
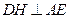 于H.由平面
于H.由平面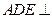 平面
平面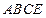 得,
得,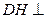 平面
平面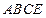 ,所以
,所以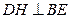 ,由题意可得
,由题意可得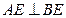 ,因此
,因此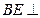 平面
平面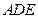 ..
..(2)在平面CDE内,过C作CE的垂线,与过D作CE的平行线交于F,再过B作
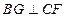 于G,连结DG,CH,BH可得
于G,连结DG,CH,BH可得 平面
平面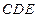 ;所以
;所以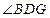 为BD和平面CDE所成的角.在
为BD和平面CDE所成的角.在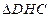 中,
中, 中,可得
中,可得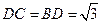 ,又
,又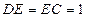 ,因此
,因此
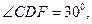
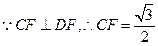 .由题意得
.由题意得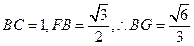 ,因此
,因此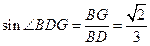 ,BD和平面
,BD和平面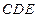 所成的角的正弦值为
所成的角的正弦值为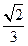 .
.
练习册系列答案
相关题目
 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ( ).
( ). 
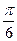



 ⊥平面
⊥平面 ,直线
,直线
 平面
平面 ,下面有三个命题:①
,下面有三个命题:①

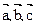 ,若
,若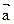 ∥
∥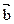 ,
,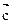 则
则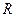 的球互相外切,且每个球都同时与另两个半径为
的球互相外切,且每个球都同时与另两个半径为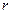 的球外切.如果这两个半径为
的球外切.如果这两个半径为



 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中, ,过
,过 作与
作与 分别交于
分别交于 和
和 的截面,则截面
的截面,则截面
 的周长的最小值是________
的周长的最小值是________