题目内容
已知线段PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点。
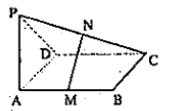
(1)求证:MN//平面PAD;
(2)当∠PDA=45°时,求证:MN⊥平面PCD;

(1)求证:MN//平面PAD;
(2)当∠PDA=45°时,求证:MN⊥平面PCD;
同解析
(1)取PD的中点E,连接AE、EN
∵EN平行且等于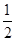 DC,而
DC,而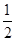 DC平行且等于AM
DC平行且等于AM
∴AMNE为平行四边形MN∥AE
∴MN∥平面PAD
(2)∵PA⊥平面ABCD∴CD⊥PA又
∵ABCD为矩形 ∴CD⊥AD, ∴CD⊥AE,AE∥MN,MN⊥CD
∵AD⊥DC,PD⊥DC ∴∠ADP=45°, 又E是斜边的PD的中点∴AE⊥PD,
∴MN⊥PD∴MN⊥CD,∴MN⊥平面PCD.
∵EN平行且等于
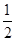 DC,而
DC,而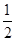 DC平行且等于AM
DC平行且等于AM ∴AMNE为平行四边形MN∥AE
∴MN∥平面PAD
(2)∵PA⊥平面ABCD∴CD⊥PA又
∵ABCD为矩形 ∴CD⊥AD, ∴CD⊥AE,AE∥MN,MN⊥CD
∵AD⊥DC,PD⊥DC ∴∠ADP=45°, 又E是斜边的PD的中点∴AE⊥PD,
∴MN⊥PD∴MN⊥CD,∴MN⊥平面PCD.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
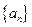 中,
中,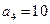 且
且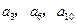 成等比数列.
成等比数列.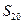 .
.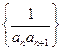 前n项的和
前n项的和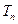 .
.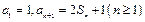
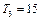 ,又
,又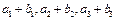 成等比数列,求Tn
成等比数列,求Tn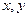 值依
值依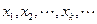 ;
;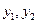 ,…,
,…,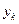 ,….
,….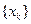 和
和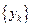 的通项公式;
的通项公式;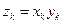 ,求数列
,求数列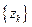 的前
的前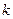 项和
项和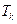 ,
,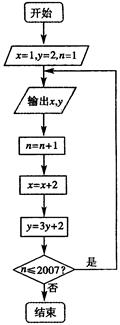 其中
其中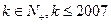 .
.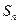
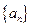

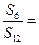
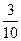
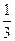

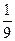
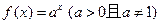 的图象上一点,数列
的图象上一点,数列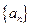 的前
的前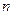 项和为
项和为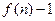 .(I)求数列
.(I)求数列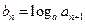 ,求数列
,求数列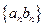 的前
的前


 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由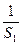 +
+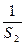 +
+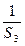 +…+
+…+ =__________.
=__________.