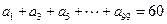题目内容
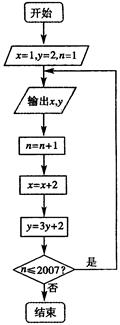
根据如图所示的程序框图,将输出的
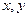 值依
值依次分别记为
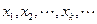 ;
;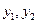 ,…,
,…,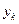 ,….
,….(Ⅰ)分别求数列
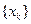 和
和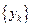 的通项公式;
的通项公式;(Ⅱ)令
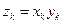 ,求数列
,求数列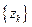 的前
的前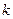 项和
项和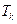 ,
, 其中
其中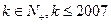 .
.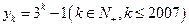 ;
;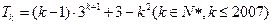
(Ⅰ)由框图,知数列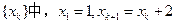
∴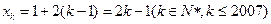
由框图,知数列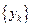 中,
中,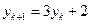 ∴
∴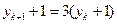
∴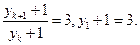 ∴数列
∴数列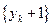 是以3为首项,3为公比的等比数列
是以3为首项,3为公比的等比数列
∴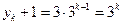 ∴
∴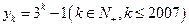
(Ⅱ)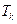 =
=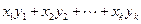
=1×(3-1)+3×(32-1)+…+(2k-1)(3k-1)
=1×3+3×32+…+(2k-1)·3k-[1+3+…+(2k-1)]
记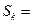 1×3+3×32+…+(2k-1)·3k,①
1×3+3×32+…+(2k-1)·3k,①
则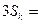 1×32+3×33+…+(2k-1)×3k+1 ②
1×32+3×33+…+(2k-1)×3k+1 ②
①-②,得-2Sk=3+2·32+2·33+…+2·3k-(2k-1)·3k+1
=2(3+32+…+3k)-3-(2k-1)·3k+1
=2×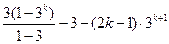
=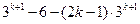
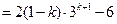
∴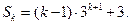
又1+3+…+(2k-1)=k2
∴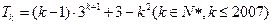
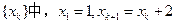
∴
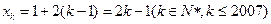
由框图,知数列
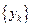 中,
中,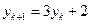 ∴
∴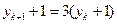
∴
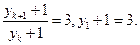 ∴数列
∴数列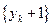 是以3为首项,3为公比的等比数列
是以3为首项,3为公比的等比数列∴
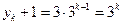 ∴
∴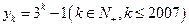
(Ⅱ)
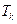 =
=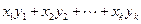
=1×(3-1)+3×(32-1)+…+(2k-1)(3k-1)
=1×3+3×32+…+(2k-1)·3k-[1+3+…+(2k-1)]
记
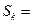 1×3+3×32+…+(2k-1)·3k,①
1×3+3×32+…+(2k-1)·3k,①则
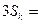 1×32+3×33+…+(2k-1)×3k+1 ②
1×32+3×33+…+(2k-1)×3k+1 ②①-②,得-2Sk=3+2·32+2·33+…+2·3k-(2k-1)·3k+1
=2(3+32+…+3k)-3-(2k-1)·3k+1
=2×
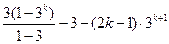
=
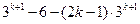
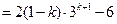
∴
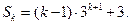
又1+3+…+(2k-1)=k2
∴
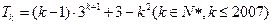

练习册系列答案
相关题目
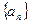 的各项均为正值,
的各项均为正值,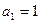 ,对任意
,对任意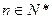 ,
,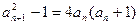 ,
,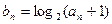 都成立.
都成立.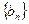 的通项公式;
的通项公式;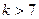 且
且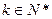 时,证明对任意
时,证明对任意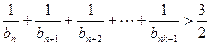 成立.
成立.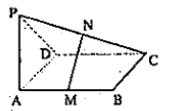
 _____________.(用π表示即可)
_____________.(用π表示即可)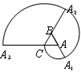
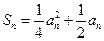
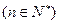 成立. (1)求数列{an}的通项公式; (2)令数列
成立. (1)求数列{an}的通项公式; (2)令数列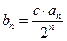 (其中c为正实数),Tn为数列{bn}的前n项和,若Tn>8对n∈N*恒成立,求c的取值范围.
(其中c为正实数),Tn为数列{bn}的前n项和,若Tn>8对n∈N*恒成立,求c的取值范围.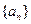
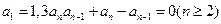
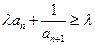 对任意
对任意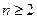 的整数恒成立,求实数
的整数恒成立,求实数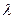 的取值范围;
的取值范围;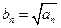 ,
,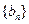 的前
的前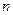 项和为
项和为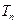 ,求证:
,求证: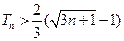



 ,试问当n为何值时,
,试问当n为何值时, 最大?并求出
最大?并求出 为整数,集合
为整数,集合 中的数由小到大组成数列
中的数由小到大组成数列 :
: ,则
,则 。
。