题目内容



⑴求数列
 的通项公式;
的通项公式;⑵设
 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;⑶是否存在以
 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由(1)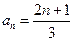 (2)
(2)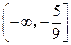 (3)
(3)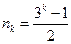
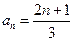 (2)
(2)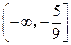 (3)
(3)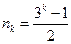
⑴因为
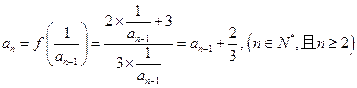 ,
,所以
 .…………………………………………………………………………2分
.…………………………………………………………………………2分因为
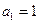 ,所以数列
,所以数列 是以1为首项,公差为
是以1为首项,公差为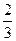 的等差数列.
的等差数列.所以
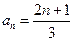 .…………………………………………………………………………4分
.…………………………………………………………………………4分⑵①当
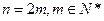 时,
时,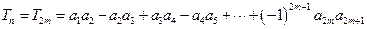

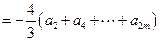

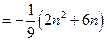 .…………………………………………………………………………6分
.…………………………………………………………………………6分②当
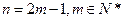 时,
时,
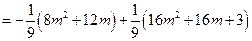
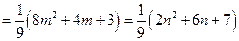 .…………………………………………8分
.…………………………………………8分所以
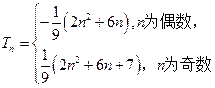
要使
 对
对 恒成立,
恒成立,只要使
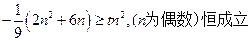 .
.只要使
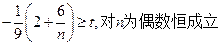 ,
,故实数
 的取值范围为
的取值范围为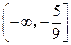 .……………………………………………………10分
.……………………………………………………10分⑶由
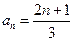 ,知数列
,知数列 中每一项都不可能是偶数.
中每一项都不可能是偶数.①如存在以
 为首项,公比
为首项,公比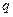 为2或4的数列
为2或4的数列 ,
, ,
,此时
 中每一项除第一项外都是偶数,故不存在以
中每一项除第一项外都是偶数,故不存在以 为首项,公比为偶数的数列
为首项,公比为偶数的数列 .……………………………………………………………………………………12分
.……………………………………………………………………………………12分②当
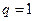 时,显然不存在这样的数列
时,显然不存在这样的数列 .
.当
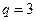 时,若存在以
时,若存在以 为首项,公比为3的数列
为首项,公比为3的数列 ,
, .
.则
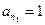 ,
,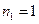 ,
,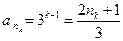 ,
,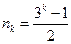 .
.所以满足条件的数列
 的通项公式为
的通项公式为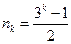 .……………………………16分
.……………………………16分
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
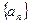 ,
,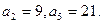
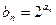 ,求数列
,求数列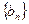 的前
的前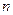 项和
项和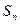 .
.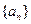
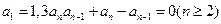
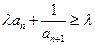 对任意
对任意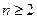 的整数恒成立,求实数
的整数恒成立,求实数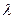 的取值范围;
的取值范围;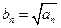 ,
,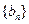 的前
的前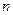 项和为
项和为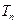 ,求证:
,求证: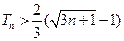
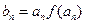 ,记数列
,记数列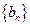 的前n项和为
的前n项和为 ,当
,当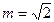 时,求
时,求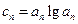 ,问是否存在实数
,问是否存在实数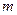 ,使得
,使得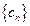 中每一项恒小于它后面的项?若存
中每一项恒小于它后面的项?若存


 ,试问当n为何值时,
,试问当n为何值时, 最大?并求出
最大?并求出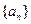 的公差
的公差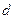 不为零,首项
不为零,首项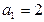 且前
且前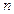 项和为
项和为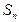 .
.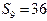 时,在数列
时,在数列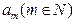 ,使得
,使得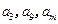 成为等比数列,求
成为等比数列,求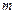 的值.
的值.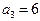 时,若自然数
时,若自然数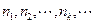 满足
满足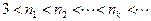 并且
并且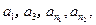
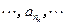 是等比数列,求
是等比数列,求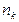 的值。
的值。