Question

在抛物线y²=-4x上求一点P，使其到焦点F的距离与到A（-2，1）的距离之和最小，则该点的坐标是______．

Answer 1

由抛物线方程为y²=-4x，可得2p=4，

p

2

=1，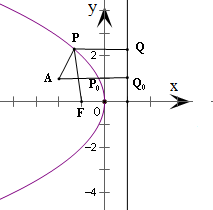
∴焦点坐标为F（-1，0），准线方程为x=1．
设点P在准线上的射影为Q，连结PQ，
则根据抛物线的定义得|PF|=|PQ|，
由平面几何知识，可知当A、P、Q三点共线时，
|PQ|+|PA|达到最小值，此时|PF|+|PA|也达到最小值．
∴|PF|+|PA|最小蝗，点P的纵坐标为1，
将P（x，1）代入抛物线方程，得1²=-4x，解得x=-

1

4

，
∴使P到A、F距离之和最小的点P坐标为（-

1

4

，1）．
故答案为：（-

1

4

，1）