题目内容
5.定义数列{xn}:x1=1,xn+1=3xn3+2xn2+xn;数列{yn}:yn=$\frac{1}{1+2{x}_{n}+3{{x}_{n}}^{2}}$;数列{zn}:zn=$\frac{2+3{x}_{n}}{1+2{x}_{n}+3{{x}_{n}}^{2}}$;若{yn}的前n项的积为P,{zn}的前n项的和为Q,那么P+Q=1.分析 通过对xn+1=3${{x}_{n}}^{3}$+2${{x}_{n}}^{2}$+xn变形可得$\frac{{x}_{n}}{{x}_{n+1}}$=$\frac{1}{1+2{x}_{n}+3{{x}_{n}}^{2}}$,累乘可得P=$\frac{{x}_{1}}{{x}_{n+1}}$,通过变形、分离分母可得zn=$\frac{1}{{x}_{n}}$-$\frac{1}{{x}_{n+1}}$,并项累加可得Q=$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{n+1}}$,进而计算可得结论.
解答 解:∵xn+1=3${{x}_{n}}^{3}$+2${{x}_{n}}^{2}$+xn,
∴$\frac{{x}_{n}}{{x}_{n+1}}$=$\frac{1}{1+2{x}_{n}+3{{x}_{n}}^{2}}$,
∴P=y1•y2•…•yn
=$\frac{{x}_{1}}{{x}_{2}}$•$\frac{{x}_{2}}{{x}_{3}}$•…•$\frac{{x}_{n}}{{x}_{n+1}}$
=$\frac{{x}_{1}}{{x}_{n+1}}$,
∵zn=$\frac{2+3{x}_{n}}{1+2{x}_{n}+{{3x}_{n}}^{2}}$
=$\frac{1+2{x}_{n}+3{{x}_{n}}^{2}-1}{{x}_{n}+2{{x}_{n}}^{2}+3{{x}_{n}}^{3}}$
=$\frac{1}{{x}_{n}}$-$\frac{1}{{x}_{n+1}}$,
∴Q=($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$)+($\frac{1}{{x}_{2}}$-$\frac{1}{{x}_{3}}$)+…+($\frac{1}{{x}_{n}}$-$\frac{1}{{x}_{n+1}}$)
=$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{n+1}}$,
∵x1=1,
∴P+Q=$\frac{{x}_{1}}{{x}_{n+1}}$+$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{n+1}}$=$\frac{1}{{x}_{n+1}}$+1-$\frac{1}{{x}_{n+1}}$=1,
故答案为:1.
点评 本题考查了经过变形利用“累乘求积”求数列的乘积、利用“累加求和”求数列的和的基本技能方法,属于难题.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | $\frac{11}{16}$ | B. | $\frac{7}{8}$ | C. | -$\frac{1}{4}$ | D. | 不确定 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 60 | B. | 40 | C. | 120 | D. | 36 |
| A. | 与g(x)的图象相同 | |
| B. | 与g(x)的图象关于y轴对称 | |
| C. | 是由g(x)的图象向左平移$\frac{π}{2}$个单位得到的 | |
| D. | 是由g(x)的图象向右平移$\frac{π}{2}$个单位得到的 |
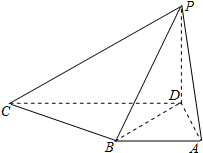 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.