题目内容
20.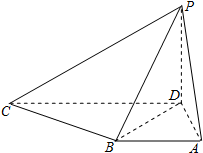 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PBD.
分析 (1)由AB∥CD,利用直线与平面平行的判定定理即可得证;
(2)可求$BD=\sqrt{2}$,由勾股定理的逆定理知,CB⊥BD,又由PD⊥底面ABCD,CB?平面ABCD,可证CB⊥PD,即可证明BC⊥平面PBD.
解答  (本小题满分13分)
(本小题满分13分)
证明:(1)∵AB∥CD,…(2分)
AB?平面PCD,CD?平面PCD…(5分)
∴AB∥平面PCD…(6分)
(2)在直角梯形ABCD中,∠BAD=90°,AB=AD=1,
∴$BD=\sqrt{2}$,…(7分)
∴BC2=(CD-AB)2+AD2=2,在△CBD中,由勾股定理的逆定理知,△CBD是直角三角形,且CB⊥BD,…(9分)
又PD⊥底面ABCD,CB?平面ABCD,
∴CB⊥PD,…(11分)
∵BD∩PD=D,∴BC⊥平面PBD.…(13分)
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于基本知识的考查.

练习册系列答案
相关题目
10.若${A}_{n}^{3}$=12${C}_{n}^{2}$,则n=( )
| A. | 8 | B. | 7 | C. | 6 | D. | 4 |
12.如果角α的终边过点(2sin$\frac{π}{6}$,-2cos$\frac{π}{6}$),则sinα的值等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |