题目内容
数列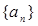 中,
中,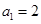 ,点
,点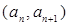 在直线
在直线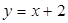 上.
上.
(Ⅰ)求证数列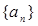 是等差数列,并求出数列
是等差数列,并求出数列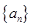 的通项公式;
的通项公式;
(Ⅱ)若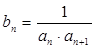 ,求数列
,求数列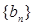 的前
的前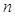 项和
项和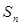 .
.
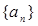 中,
中,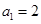 ,点
,点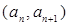 在直线
在直线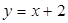 上.
上.(Ⅰ)求证数列
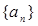 是等差数列,并求出数列
是等差数列,并求出数列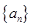 的通项公式;
的通项公式;(Ⅱ)若
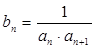 ,求数列
,求数列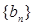 的前
的前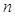 项和
项和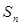 .
.(Ⅰ)证明:依题意可得:
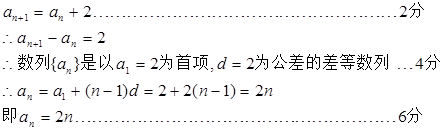
(Ⅱ)解:由(Ⅰ)可得: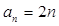

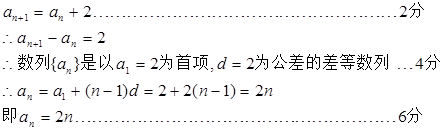
(Ⅱ)解:由(Ⅰ)可得:
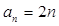

略

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
题目内容
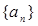 中,
中,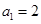 ,点
,点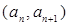 在直线
在直线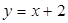 上.
上.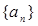 是等差数列,并求出数列
是等差数列,并求出数列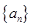 的通项公式;
的通项公式;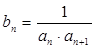 ,求数列
,求数列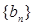 的前
的前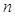 项和
项和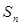 .
.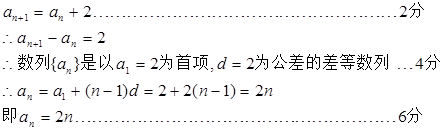
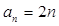


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案