题目内容
15.向量$\overrightarrow a,\overrightarrow b$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=4,则|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的最大值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 利用向量的数量积公式求出$\overrightarrow{a}$2=|$\overrightarrow{a}$|2;再利用向量模的平方等于向量的平方求出|$\overrightarrow{a}$$+\overrightarrow{b}$|,根据模的几何意义得出$\overrightarrow{a}$$+\overrightarrow{b}$与$\overrightarrow{c}$方向相反时|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|取最大值,
解答 解:∵量$\overrightarrow a,\overrightarrow b$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2×2×cos120°=-2,
|$\overrightarrow{a}$$+\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2$+2\overrightarrow{a}•\overrightarrow{b}$=4+4-4=4,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2
∵|$\overrightarrow{c}$|=4,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|≤|$\overrightarrow{a}$$+\overrightarrow{b}$|+|$\overrightarrow{c}$|=2+4=6($\overrightarrow{a}$$+\overrightarrow{b}$与$\overrightarrow{c}$方向相反时等号成立)
故选:C.
点评 本题考查向量的数量积公式、向量模的性质:向量模的平方等于向量的平方,向量的模的几何意义.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
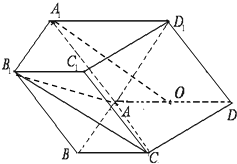 如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点. 如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且PA=AB=2,E为PE中点.
如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且PA=AB=2,E为PE中点.