题目内容
3. 如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且PA=AB=2,E为PE中点.
如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且PA=AB=2,E为PE中点.(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)证明:平面PCD⊥平面PAD;
(Ⅲ)求EA和平面ABCD所成的角;
(Ⅳ)求二面角E-AC-D的正切值.
分析 (Ⅰ)设BD∩AC=O,则由题意可得OE为△PBD的中位线,故有OE∥PB,根据直线和平面平行的判定定理证得PB∥平面AEC.
(Ⅱ)证明PA⊥CD,且AD⊥CD,证得CD⊥平面PAD.再利用平面和平面垂直的判定定理证得平面PCD⊥平面PAD.
(Ⅲ)取AD得中点H,证得∠EAH为EA和平面ABCD所成的角.由条件求得tan∠EAH=$\frac{EH}{AH}$=1,可得∠EAH 的值.
(Ⅳ)作HM⊥AC,M为垂足,可得∠EMH为二面角E-AC-D的平面角.再根据tan∠EMH=$\frac{EH}{HM}$,计算求的结果.
解答 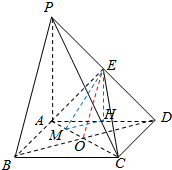 解:(Ⅰ)证明:设BD∩AC=O,则由四边形ABCD为正方形,可得O为BD的中点,
解:(Ⅰ)证明:设BD∩AC=O,则由四边形ABCD为正方形,可得O为BD的中点,
再根据E为PE中点,可得OE为△PBD的中位线,故有OE∥PB.
而OE?平面AEC,PB?平面AEC,∴PB∥平面AEC.
(Ⅱ)证明:∵PA⊥平面ABCD,∴PA⊥CD,又正方形ABCD中,AD⊥CD,
且PA∩AD=A,∴CD⊥平面PAD.
再根据CD?平面PCD,可得平面PCD⊥平面PAD.
(Ⅲ)取AD得中点H,则EH是△PAD的中位线,故有EH∥PA.
由PA⊥平面ABCD 可得EH⊥平面ABCD,∴∠EAH为EA和平面ABCD所成的角.
由PA=AB=2,可得EH=1,AH=1,∴tan∠EAH=$\frac{EH}{AH}$=1,∴∠EAH=$\frac{π}{4}$,
即EA和平面ABCD所成的角为$\frac{π}{4}$.
(Ⅳ)作HM⊥AC,M为垂足,由三垂线定理可得EM⊥AC,∠EMH为二面角E-AC-D的平面角.
由于HM=$\frac{1}{2}$DO=$\frac{\sqrt{2}}{2}$,∴tan∠EMH=$\frac{EH}{HM}$=$\frac{1}{\frac{\sqrt{2}}{2}}$=$\sqrt{2}$.
点评 本题主要考查直线和平面平行的判定定理,平面和平面垂直的判定定理,直线和平面所成的角、二面角的定义和求法,属于中档题.

| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)根据上表数据用最小二乘法求出y关于x的线性回归方程.
(3)由(2)预测技改后生产100吨甲产品的生产能耗是多少吨标准煤?(参考数值:3*2.5+4*3+5*4+6*4.5=66.5)