题目内容
5.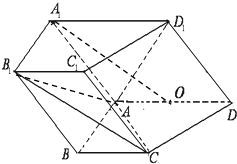 如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.(1)求证:A1O∥平面AB1C;
(2)求三棱锥B1-ABC的体积.
分析 (1)欲证A1O∥平面AB1C,根据直线与平面平行的判定定理可知只需证A1O与平面AB1C内一直线平行,连接CO、A1O、AC、AB1,利用平行四边形可证A1O∥B1C,又A1O?平面AB1C,B1C⊆平面AB1C,满足定理所需条件;
(2)由题意,B1到平面ABC的距离等于D1到平面ABC的距离即D1O=1,即可求出三棱锥B1-ABC的体积.
解答 (1)证明:如图(1),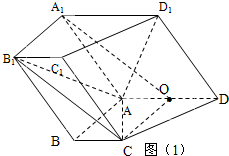
连接CO、A1O、AC、AB1,
则四边形ABCO为正方形,所以OC=AB=A1B1,
所以,四边形A1B1CO为平行四边形,
所以A1O∥B1C,
又A1O?平面AB1C,B1C⊆平面AB1C
所以A1O∥平面AB1C;
(2)解:由题意,B1到平面ABC的距离等于D1到平面ABC的距离即D1O=1,
所以三棱锥B1-ABC的体积为$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$.
点评 本题主要考查了线面平行的判定,以及利用空间向量的方法求解二面角等有关知识,同时考查了空间想象能力、转化与划归的思想,属于中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
16.由“0”、“1”、“2”组成的三位数码组中,若用A表示“第二位数字为0”的事件,用B表示“第一位数字为0”的事件,则P(A|B)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
14.在正方体ABCD-A1B1C1D1中,B1C与对角面DD1B1B所成角的大小是( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
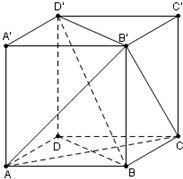 正方体ABCD-A′B′C′D′中,求证:
正方体ABCD-A′B′C′D′中,求证: