题目内容
7．数列{an}中，已知a1=1，a2=2，an+2=an+1-an（n∈N*），则a2015=（ ）| A． | 1 | B． | -1 | C． | -2 | D． | 2 |
分析 由a1=1，a2=2，an+2=an+1-an可判断数列{an}的周期为6，从而求得．
解答 解：∵a1=1，a2=2，an+2=an+1-an，
∴a3=a2-a1=2-1=1，
a4=a3-a2=1-2=-1，
a5=a4-a3=-1-1=-2，
a6=a5-a4=-2-（-1）=-1，
a7=a6-a5=-1-（-2）=1，
a8=a7-a6=1-（-1）=2，
∴数列{an}的周期为6，且2015=335×6+5，
∴a2015=a5=-2；
故选C．
点评 本题考查了数列的递推公式的应用及数列周期性的应用，属于中档题．
练习册系列答案
优生乐园系列答案
相关题目
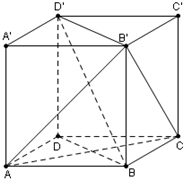正方体ABCD-A′B′C′D′中，求证：