题目内容
【题目】在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面是边长是1的正方形，侧棱PA与底面成45°的角，M，N，分别是AB，PC的中点；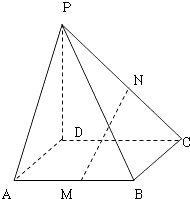 
（1）求证：MN∥平面PAD；
（2）求四棱锥P﹣ABCD的体积．
【答案】
（1）证明：设PD的中点为E，连NE，AE
根据三角形的中位线可知NE∥CD，且NE= 
CD，
AM∥CD，且AM= CD，
∴NE∥AM，且NE=AM
∴MN∥AE，
AE平面PAD，MN平面PAD，
∴MN∥平面PAD
（2）解：四棱锥P﹣ABCD的底面积为1，
因为PD⊥平面ABCD，所以四棱锥P﹣ABCD的高为1，
所以四棱锥P﹣ABCD的体积为： 
【解析】（1）欲证MN∥平面PAD，根据直线与平面平行的判定定理可知只需证MN与平面PAD内一直线平行，根据三角形的中位线可知PC∥EO，满足定理条件；（2）根据四棱锥P﹣ABCD的底面积为1，高为PD，即可求出四棱锥P﹣ABCD的体积．
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)．
练习册系列答案
相关题目
