题目内容
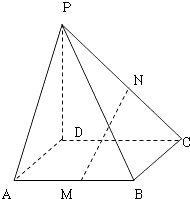
【题目】如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点. 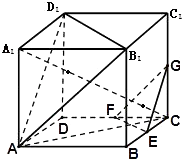
(1)求直线 A1C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG.
【答案】
(1)解:∵A1C∩平面ABCD=C,在正方体ABCD﹣A1B1C1D1中A1A⊥平面ABCD
∴AC为A1C在平面ABCD的射影
∴∠A1CA为A1C与平面ABCD所成角 ![]() 正方体的棱长为a∴AC=
正方体的棱长为a∴AC= ![]() a,A1C=
a,A1C= ![]() a
a
(2)证明:在正方体ABCD﹣A1B1C1D1中
连接BD,则DD1∥BB1,DD1=BB1,
∴D1DBB1为平行四边形
∴D1B1∥DB
∵E,F分别为BC,CD的中点
∴EF∥BD∴EF∥D1B1
∵EF平面GEF,D1B1平面GEF
∴D1B1∥平面GEF
同理AB1∥平面GEF
∵D1B1∩AB1=B1
∴平面AB1D1∥平面EFG.
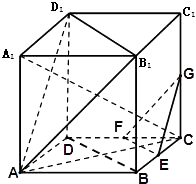
【解析】(1)欲求直线 A1C与平面ABCD所成角的正弦的值,在正方体ABCD﹣A1B1C1D1中,由于AC为A1C在平面ABCD的射影,故∠A1CA为A1C与平面ABCD所成角,最后在直角三角形中求解即得;(2)欲证平面AB1D1∥平面EFG,根据面面平行的判定定理可知,只须证明线面平行即可.在正方体ABCD﹣A1B1C1D1中连接BD,则DD1∥BB1 , DD1=BB1 , 利用直线间的平行关系可证得:D1B1∥平面GEF及AB1∥平面GEF,从而问题解决.
【考点精析】解答此题的关键在于理解平面与平面平行的判定的相关知识,掌握判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目