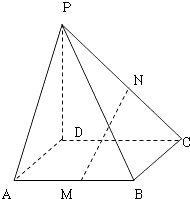
题目内容
【题目】已知椭圆x2+4y2=4,直线l:y=x+m
(1)若l与椭圆有一个公共点,求m的值;
(2)若l与椭圆相交于P、Q两点,且|PQ|等于椭圆的短轴长,求m的值.
【答案】
(1)解:把直线y=x+m代入椭圆方程得:x2+4(x+m)2=4,即:5x2+8mx+4m2﹣4=0,
△=(8m)2﹣4×5×(4m2﹣4)=﹣16m2+80=0
解得:m= ![]()
(2)解:设该直线与椭圆相交于两点A(x1,y1),B(x2,y2),
则x1,x2是方程5x2+8mx+4m2﹣4=0的两根,
由韦达定理可得:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
∴|AB|= ![]() =
= ![]() =
= ![]() =2;
=2;
∴m=± ![]()
【解析】(1)将直线的方程y=x+m与椭圆的方程x2+4y2=4联立,得到5x2+2mx+m2﹣1=0,利用△=0,即可求得m的取值范围;(2)利用两点间的距离公式,再借助于韦达定理即可得到:两交点AB之间的距离,列出|AB|=2,从而可求得m的值.

【题目】雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:
PM2.5日均值 | 0﹣﹣35 | 35﹣﹣75 | 75﹣﹣115 | 115﹣﹣150 | 150﹣﹣250 | 250以上 |
空气质量等级 | 1级 | 2级 | 3级 | 4级 | 5级 | 6级 |
由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据,用茎叶图表示,如图所示.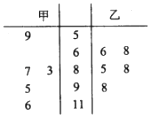
(1)试根据统计数据,分别写出两城区的PM2.5日均值的中位数,并从中位数角度判断哪个城区的空气质量较好?
(2)考虑用频率估计概率的方法,试根据统计数据,估计甲城区某一天空气质量等级为3
(3)分别从甲、乙两个城区的统计数据中任取一个,试求这两城区空气质量等级相同的概率.