题目内容
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定: ![]() 、
、![]() 、
、![]() 三级为合格等级,
三级为合格等级, ![]() 为不合格等级.
为不合格等级.
百分制 |
|
|
|
|
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图
的分组作出频率分布直方图如图![]() 所示,样本中分数在
所示,样本中分数在![]() 分及以上的所有数据的茎叶图如图
分及以上的所有数据的茎叶图如图![]() 所示.
所示.
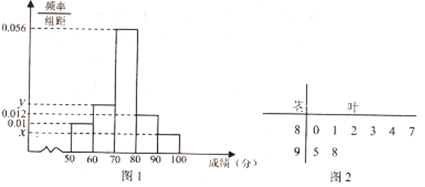
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选![]() 人,求至少有
人,求至少有![]() 人成绩是合格等级的概率;
人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 、
、![]() 两个等级的学生中随机抽取了
两个等级的学生中随机抽取了![]() 名学生进行调研,记
名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)分布列见解析,
;(III)分布列见解析, ![]() .
.
【解析】试题分析:(I)借助题设条件运用频率分布直方图求解;(II)依据题设对立事件的概率公式求解;(III)依据题设运用随机变量的数学期望公式探求.
试题解析:
(Ⅰ)由题意可知,样本容量![]()
![]()
(Ⅱ)成绩是合格等级人数为:![]() 人,抽取的50人中成绩是合格等级的频率为
人,抽取的50人中成绩是合格等级的频率为![]() ,故从该校学生中任选1人,成绩是合格等级的概率为
,故从该校学生中任选1人,成绩是合格等级的概率为![]() ,
,
设在该校高一学生中任选3人,至少有1人成绩是合格等级的事件为![]() ,
,
则![]() ;
;
(Ⅲ)由题意知等级的学生人数为![]() 人,
人,![]() 等级的人数为人,故
等级的人数为人,故![]() 的取值为0,1,2,3,
的取值为0,1,2,3,
![]() ,
,
![]()
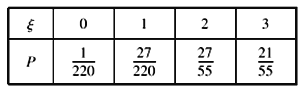
所以![]() 的分布列为:
的分布列为:
![]()

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 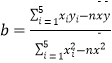 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.