题目内容
如图,过点P(1,0)作曲线C: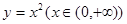 的切线,切点为
的切线,切点为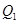 ,设点
,设点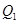 在
在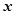 轴上的投影是点
轴上的投影是点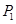 ;又过点
;又过点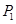 作曲线
作曲线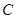 的切线,切点为
的切线,切点为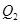 ,设
,设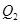 在
在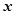 轴上的投影是
轴上的投影是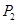 ;………;依此下去,得到一系列点
;………;依此下去,得到一系列点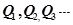
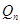 ,设点
,设点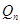 的横坐标为
的横坐标为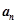 .
.
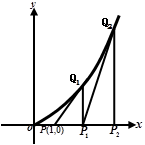
(1)求直线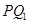 的方程;
的方程;
(2)求数列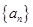 的通项公式;
的通项公式;
(3)记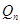 到直线
到直线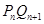 的距离为
的距离为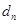 ,求证:
,求证: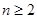 时,
时,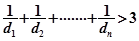
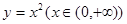 的切线,切点为
的切线,切点为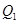 ,设点
,设点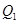 在
在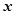 轴上的投影是点
轴上的投影是点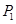 ;又过点
;又过点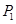 作曲线
作曲线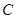 的切线,切点为
的切线,切点为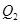 ,设
,设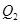 在
在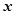 轴上的投影是
轴上的投影是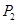 ;………;依此下去,得到一系列点
;………;依此下去,得到一系列点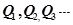
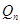 ,设点
,设点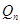 的横坐标为
的横坐标为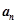 .
.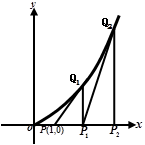
(1)求直线
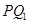 的方程;
的方程;(2)求数列
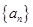 的通项公式;
的通项公式;(3)记
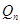 到直线
到直线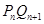 的距离为
的距离为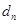 ,求证:
,求证: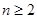 时,
时,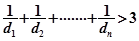
(1)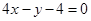
(2)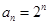
(3)根据点到直线的距离公式来放缩得到证明。
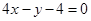
(2)
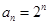
(3)根据点到直线的距离公式来放缩得到证明。
试题分析:解:(1)令
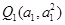 ,由
,由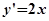 得
得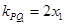 1分
1分即
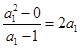 故
故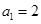 2分
2分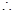
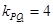 ,则切线
,则切线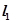 的方程为:
的方程为: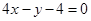 4分
4分(2)令
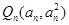 ,则
,则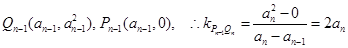 5分
5分化简得
 , 6分
, 6分故数列
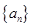 是以2为首项2为公比的等比数列 7分
是以2为首项2为公比的等比数列 7分所以
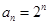 9分
9分(3)由(2)知
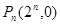 ,
,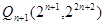 ,
,
故
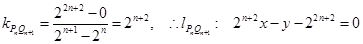 10分
10分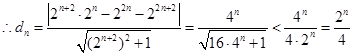 11分
11分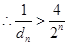 12
12故
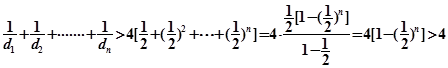 14分
14分点评:主要是考查了数列于解析几何的综合运用,属于难度题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
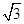 x+1的倾斜角的
x+1的倾斜角的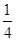 ,且分别满足下列条件的直线方程:
,且分别满足下列条件的直线方程: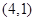 ,B
,B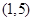 ,C
,C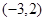 ;
;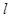 经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线
经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线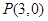 作直线
作直线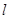 ,使它被两相交直线
,使它被两相交直线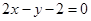 和
和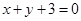 所截得的线段
所截得的线段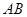 恰好被
恰好被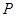 点平分,求直线
点平分,求直线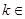 R,直线
R,直线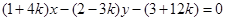 恒过一定点P,若直线
恒过一定点P,若直线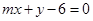 也过点P,则m = .
也过点P,则m = .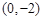 的直线L与以
的直线L与以 、
、 为端点的线段有公共点,则直线L的斜率k的取值范围是( )
为端点的线段有公共点,则直线L的斜率k的取值范围是( )