题目内容
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1)若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,4],b∈[0,6],求方程没有实根的概率.
(1)若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,4],b∈[0,6],求方程没有实根的概率.
(1)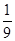 (2)
(2)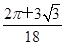
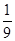 (2)
(2)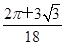
设“方程有两个正根”的事件为A,“方程没有实根”的事件为B.
(1)由题意知本题是一个古典概型,用(a,b)表示一枚骰子掷两次所得到的点数.依题意知,基本事件(a,b)的总数有36个,二次方程x2-2(a-2)x-b2+16=0有两正根,等价于
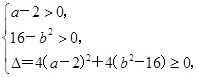 即
即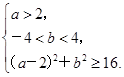 则事件A包含的基本事件为(6,1)、(6,2)、(6,3)、(5,3)共4个.∴所求的概率为P(A)=
则事件A包含的基本事件为(6,1)、(6,2)、(6,3)、(5,3)共4个.∴所求的概率为P(A)=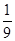 .
.
(2)由题意知本题是一个几何概型,试验的全部结果构成区域Ω={(a,b)|2≤a≤4,0≤b≤6},其面积为S(Ω)=12.满足条件的事件为:B={(a,b)|2≤a≤4,0≤b≤6,(a-2)2+b2<16},其面积为S(B)=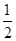 ×
×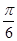 ×4×4+
×4×4+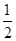 ×2×
×2×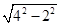 =
=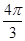 +2
+2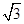 .
.
∴所求的概率P(B)=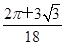 .
.
(1)由题意知本题是一个古典概型,用(a,b)表示一枚骰子掷两次所得到的点数.依题意知,基本事件(a,b)的总数有36个,二次方程x2-2(a-2)x-b2+16=0有两正根,等价于
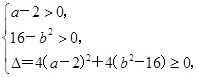 即
即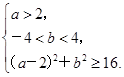 则事件A包含的基本事件为(6,1)、(6,2)、(6,3)、(5,3)共4个.∴所求的概率为P(A)=
则事件A包含的基本事件为(6,1)、(6,2)、(6,3)、(5,3)共4个.∴所求的概率为P(A)=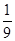 .
.(2)由题意知本题是一个几何概型,试验的全部结果构成区域Ω={(a,b)|2≤a≤4,0≤b≤6},其面积为S(Ω)=12.满足条件的事件为:B={(a,b)|2≤a≤4,0≤b≤6,(a-2)2+b2<16},其面积为S(B)=
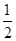 ×
×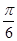 ×4×4+
×4×4+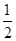 ×2×
×2×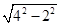 =
=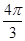 +2
+2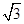 .
.∴所求的概率P(B)=
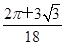 .
.
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
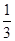

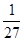
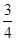
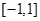 上随机取一个数x,
上随机取一个数x,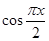 的值介于0到
的值介于0到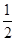 之间的概率为
之间的概率为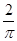

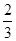

 内任取一点P,则点P落在单位圆
内任取一点P,则点P落在单位圆 内的概率为 ;
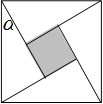
内的概率为 ;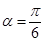 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是______________.
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是______________.