题目内容
（本小题满分12分）
三棱柱ABC—A1B1C1中，CC1⊥平面ABC，△ABC是边长为2的等边三角形，D为AB边中点，且CC1="2AB."
（1）求证：平面C1CD⊥平面ABC；
（2）求证：AC1∥平面CDB1；
（3）求三棱锥D—CBB1的体积.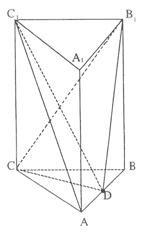
三棱柱ABC—A1B1C1中，CC1⊥平面ABC，△ABC是边长为2的等边三角形，D为AB边中点，且CC1="2AB."
（1）求证：平面C1CD⊥平面ABC；
（2）求证：AC1∥平面CDB1；
（3）求三棱锥D—CBB1的体积.
（1）证明见解析
（2）证明见解析
（3）
（2）证明见解析
（3）
（1）证明：因为CC1⊥平面ABC，
又CC1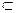
平面C1CD，
所以平面C1CD⊥平面ABC。 ………………4分
（2）证明：连结BC1交B1C于O，连结DO。
则O是BC1的中点，
DO是△BAC1的中位线。
所以DO//AC1。 …………6分
因为DO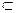平面CDB1。 ………………8分
（3）解：因为CC⊥平面ABC，
所以BB1⊥平面ABC，
所以BB
1为三棱锥D—CBB1的高。 ………………10分
所以三棱锥D—CBB1的体积为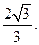
………………12分
又CC1
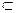平面C1CD，所以平面C1CD⊥平面ABC。 ………………4分
（2）证明：连结BC1交B1C于O，连结DO。
则O是BC1的中点，
DO是△BAC1的中位线。
所以DO//AC1。 …………6分
因为DO
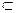平面CDB1。 ………………8分（3）解：因为CC⊥平面ABC，
所以BB1⊥平面ABC，
所以BB
1为三棱锥D—CBB1的高。 ………………10分所以三棱锥D—CBB1的体积为
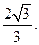………………12分
练习册系列答案
相关题目
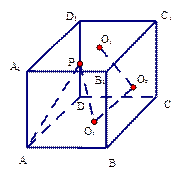
中，P为DD1中点，O1、O2、O3分别为面
、面
、面
的中心。（1）求证：
。
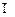BD = O，A1C1
B1D1 = O1，E是O1A的中点．
、
、
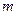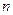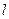是三条不同的直线，
、
、
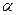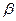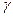是三个不同的平面，则下列命题正确的是（ ）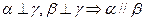
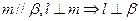
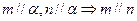
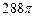的球内有一个内接正三棱锥
，球心恰好在底面正△
内，一个动点从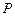
点出发沿球面运动，经过其余三点后返回，则经过的最短路程为__________
圈上有甲、已两地，甲地位于东径
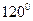，乙地位于西径
，则地球（半径为R）表面上甲、乙两地的最短距离为_________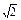 
a，则它的5个面中，互相垂直的面有 对.
，
，
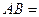
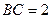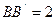，N、M分别是
、
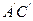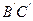的中点
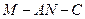的余弦值