题目内容
【题目】已知函数f(x)是二次函数,且满足f(0)=1,f(x+1)﹣f(x)=2x+5;函数g(x)=ax(a>0且a≠1)
(1)求f(x)的解析式;
(2)若g(2)= ![]() ,且g[f(x)]≥k对x∈[﹣1,1]恒成立,求实数k的取值范围.
,且g[f(x)]≥k对x∈[﹣1,1]恒成立,求实数k的取值范围.
【答案】
(1)解:∵f(x+1)﹣f(x)=2x+5,
∴f(1)﹣f(0)=5,f(2)﹣f(1)=7,
又f(0)=1,∴f(1)=6,f(2)=13.
设f(x)=mx2+bx+c,
则 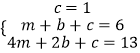 ,解得m=1,b=4.
,解得m=1,b=4.
∴f(x)=x2+4x+1
(2)解:∵g(2)=a2= ![]() ,∴a=
,∴a= ![]() .
.
∴g[f(x)]=( ![]() )
) ![]() ,
,
∵f(x)=x2+4x+1在[﹣1,1]上单调递增,g(x)是减函数,
∴g(f(x))在[﹣1,1]上是减函数,
g(f(x))在[﹣1,1]上的最小值为g(f(1))=g(6)= ![]() =
= ![]() .
.
∵g[f(x)]≥k对x∈[﹣1,1]恒成立,
∴k≤ ![]()
【解析】(1)利用关系式求出f(1),f(2),利用待定系数法求出f(x);(2)求出a的值,判断g(f(x))的单调性,根据单调性得出g(f(x))在[﹣1,1]上的最小值,从而得出k的范围.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.

练习册系列答案
相关题目
