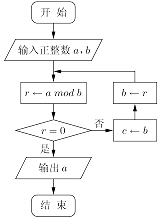
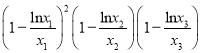题目内容
【题目】如图,A是△BCD所在平面外一点,M、N为△ABC和△ACD重心,BD=6; 
(1)求MN的长;
(2)若A、C的位置发生变化,MN的位置和长度会改变吗?
【答案】
(1)解:延长AM、AN,分别交BC、CD于点E、F,连结EF.
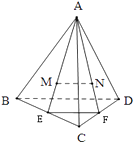
∵M、N分别是△ABC和△ACD的重心,
∴AE、AF分别为△ABC和△ACD的中线,且 ![]() =
= ![]() ,
,
可得MN∥EF且MN= ![]() EF,
EF,
∵EF为△BCD的中位线,可得EF= ![]() BD,
BD,
∴MN= ![]() BD=2
BD=2
(2)解:由(1)可得位置改变,长度不改变.
【解析】(1)利用三角形的重心的性质,可得M、N分别是△ABC与△ACD的中线的一个三等分点,得 ![]() =
= ![]() ,由此利用平行线的性质与三角形中位线定理,算出MN与BD的关系,即可得到MN的长.(2)由(1)可得位置改变,长度不改变.
,由此利用平行线的性质与三角形中位线定理,算出MN与BD的关系,即可得到MN的长.(2)由(1)可得位置改变,长度不改变.
【考点精析】本题主要考查了棱锥的结构特征的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方才能正确解答此题.

练习册系列答案
相关题目