Question

【题目】已知函数f（x）=ax2﹣ x+c（a，c∈R）满足条件：①f（1）=0；②对一切x∈R，都有f（x）≥0
（1）求a、c的值；
（2）若存在实数m，使函数g（x）=f（x）﹣mx在区间[m，m+2]上有最小值﹣5，求出实数m的值．

Answer 1

【答案】
（1）解：法一：当a=0时，f（x）=﹣ x+c．

由f（1）=0得：﹣ +c=0，即c= ，∴f（x）=﹣ x+ ．

显然x＞1时，f（x）＜0，这与条件②相矛盾，不合题意．

∴a≠0，函数f（x）=ax2﹣ x+c是二次函数．

由于对一切x∈R，都有f（x）≥0，于是由二次函数的性质可得：

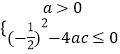，即 （*），

由f（1）=0得 a+c= ，即c= ﹣a，代入（*）得 a（ ﹣a）≥

整理得 a2﹣ a+ ≤0，即（a﹣ ）2≤0．

而（a﹣ ）2≥0，∴a= ，

将a= 代入（*）得，c= ，

∴a=c= ．

法二：当a=0时，f（x）=﹣ x+c．

由f（1）=0得﹣ +c=0，即c= ，

∴f（x）=﹣ x+ ，

显然x＞1时，f（x）＜0，这与条件②相矛盾，

∴a≠0，因而函数f（x）=a2﹣ x+c是二次函数．

由于对一切x∈R，都有f（x）≥0，于是由二次函数的性质可得：

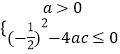，由此可知 a＞0，c＞0，

∴ac≤（ ）2．

由f（1）=0，得 a+c= ，代入上式得 ac≤ ，

但前面已推得 ac≥ ，

∴ac= ，

由 解得 a=c=

（2）解：∵a=c= ，∴f（x）= x2﹣ x+ ．

∴g（x）=f（x）﹣mx= x2﹣（vm）x+ ．

该函数图象开口向上，且对称轴为x=2m+1．

假设存在实数m使函数g（x）=f（x）﹣mx= x2﹣（ +m）x+ 在区间[m，m+2]上有最小值﹣5．

①当m＜﹣1时，2m+1＜m，函数g（x）在区间[m，m+2]上是递增的，

∴g（m）=﹣5，

即 m2﹣（ +m）m+ =﹣5，

解得 m=﹣3或m= ，

∵ ＞﹣1，∴m= 舍去

②当﹣1≤m＜1时，m≤2m+1＜m+1，

函数g（x）在区间[m，2m+1]上是递减的，而在区间[2m+1，m+2]上是递增的，

∴g（2m+1）=﹣5，

即 （2m+1）2﹣（ +m）（2m+1）+ =﹣5．

解得 m=﹣ ﹣ 或m=﹣ + ，均应舍去．

③当m≥1时，2m+1≥m+2，函数g（x）在区间[m，m+2]上是递减的，

∴g（m+2）=﹣5，

即 （m+2）2﹣（ +m）（m+2）+ =﹣5．

解得 m=﹣1﹣2 或m=﹣1+2 ，其中m=﹣1﹣2 应舍去．

综上可得，当m=﹣3或m=﹣1+2 时，函数g（x）=f（x）﹣mx在区间[m，m+2]上有最小值

【解析】（1）首先函数f（x）=ax2﹣ x+c是二次函数，再利用二次函数的性质解决对一切x∈R，都有f（x）≥0；根据f（1）=0得 a+c= ，即c= ﹣a，从而可得 a（ ﹣a）≥ ，进而可得a，c的值， 另解：首先函数f（x）=ax2﹣ x+c是二次函数，再利用二次函数的性质解决对一切x∈R，都有f（x）≥0；由f（1）=0，得 a+c= ，代入上式得 ac≤ ，根据 ac≥ ，可得ac= ，从而得到关于a，c的方程组，故可求a、c的值；（2）g（x）=f（x）﹣mx= x2﹣（ +m）x+ ， x2﹣（ +m）x+ 在区间[m，m+2]上有最小值﹣5．根据函数的对称轴与区间的关系进行分类讨论，从而可求m的值．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．