Question

【题目】已知圆C的方程（x﹣1）2+y2=1，P是椭圆 =1上一点，过P作圆的两条切线，切点为A，B，则 的取值范围为（ ）
A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：设PA与PB的夹角为2α，
则|PA|=PB|= ，
∴y= =| || |cos2α= cos2α
= cos2α．
记cos2α=u，则y= =﹣3+（1﹣u）+ ≥2 ﹣3，
∵P在椭圆的左顶点时，sinα= ，∴cos2α= ，
∴ 的最大值为 = ，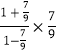
∴ 的范围为[2 ﹣3， ]，
故选：A．
由圆切线的性质，即与圆心切点连线垂直设出一个角，通过解直角三角形求出PA，PB的长；利用向量的数量积公式表示出 ，利用三角函数的二倍角公式化简函数，通过换元，再利用基本不等式求出最值．