题目内容
6.已知函数f(x)=a1nx+bx(a,b∈R)的图象在点(1,f(1))处的切线方程为 x-2y-2=0.(1)求a,b的值;
(2)当x>1时,f(x)+$\frac{k}{x}$<0恒成立.求实数k的取值范围;
(3)证明:当x∈N*,且n≥2时.$\frac{1}{2ln2}$+$\frac{1}{3ln3}$+…+$\frac{1}{nlnn}$>$\frac{{3n}^{2}-n-2}{{2n}^{2}+2n}$.
分析 (1)利用函数在点(1,f(1))处的导数值即曲线切线的斜率及点在曲线上求得a,b的值;
(2)当x>1时,f(x)+$\frac{k}{x}$<0恒成立,等价于k<0.5x2-xlnx,构造函数,求最值,即可求实数k的取值范围;
(3)利用(2)证明$\frac{1}{xlnx}$>$\frac{2}{{x}^{2}-1}$=$\frac{1}{x-1}$-$\frac{1}{x+1}$,把x=2,3,…n分别代入上面不等式,并相加得结论成立.
解答 (1)解:∵f(x)=alnx+bx,
∴f′(x)=$\frac{a}{x}$+b.
∵直线x-2y-2=0的斜率为0.5,且过点(1,-0.5),
∴f(1)=b=-0.5,f′(1)=a+b=0.5,
解得a=1,b=-0.5.
(2)解:由(1)得f(x)=lnx-0.5x.
当x>1时,f(x)+$\frac{k}{x}$<0恒成立,等价于k<0.5x2-xlnx.
令g(x)=0.5x2-xlnx,则g′(x)=x-1-lnx.
令h(x)=x-1-lnx,则h′(x)=$\frac{x-1}{x}$.
当x>1时,h′(x)>0,函数h(x)在(1,+∞)上单调递增,
故h(x)>h(1)=0,
从而,当x>1时,g′(x)>0,即函数g(x)在(1,+∞)上单调递增,
故g(x)>g(1)=0.5.
∴k≤0.5.
(3)证明:由(2)得,当x>1时,lnx-0.5x+$\frac{1}{2x}$<0,可化为xlnx<$\frac{{x}^{2}-1}{2}$,
又xlnx>0,
从而$\frac{1}{xlnx}$>$\frac{2}{{x}^{2}-1}$=$\frac{1}{x-1}$-$\frac{1}{x+1}$.
把x=2,…n分别代入上面不等式,并相加得,
$\frac{1}{2ln2}$+$\frac{1}{3ln3}$+…+$\frac{1}{nlnn}$>1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$
=1+$\frac{1}{2}$-$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{{3n}^{2}-n-2}{{2n}^{2}+2n}$.
即有原不等式成立.
点评 本题属导数的综合应用题,考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的最值,考查不等式的证明,有难度.

| A. | 是减函数,且f(x)>0 | B. | 是减函数,且f(x)<0 | C. | 是增函数,且f(x)>0 | D. | 是增函数,且f(x)<0 |
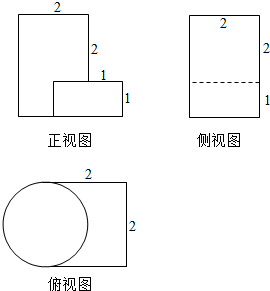
| A. | 4+$\frac{5π}{2}$ | B. | 4+$\frac{3π}{2}$ | C. | 4+$\frac{π}{2}$ | D. | 4+π |