题目内容
16.已知:在△ABC中,acosB=bcosA,则此三角形的形状为( )| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰或直角三角形 | D. | 等腰直角三角形 |
分析 根据正弦定理化简acosB=bcosA,利用两角差的正弦公式化简,根据三角形内角的范围判断出△ABC的形状.
解答 解:由题意知,在△ABC中,acosB=bcosA,
∴根据正弦定理得:sinAcosB=sinBcosA,
∴sinAcosB-sinBcosA=0,则sin(A-B)=0,
∵A、B∈(0,π),∴-π<A-B<π,
∴A-B=0,则A=B,
∴△ABC是等腰三角形,
故选:A.
点评 本题考查正弦定理,以及两角差的正弦公式的应用,注意内角的范围,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列有关命题说法正确的是( )
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 所有常数列既是等差数列也是等比数列 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 命题“?x∈R,x2+x<0”的否定是“?x∈R,x2+x≥0”. |
4.已知点P(-3,4)在角α的终边上,则$\frac{sinα+cosα}{3sinα+2cosα}$的值为( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{18}$ | D. | -1 |
11.设f(x)=x2+bx+c,且f(-1)=f(3),则( )
| A. | f(1)>c>f(-1) | B. | f(1)<c<f(-1) | C. | f(1)>f(-1)>c | D. | f(1)<f(-1)<c |
1.若函数f(x)的定义域为[0,3],则f(x2-1)的定义域为( )
| A. | [0,9] | B. | [0,8] | C. | [-2,-1]∪[1,2] | D. | [1,2] |
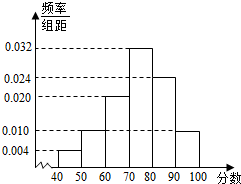 某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.