题目内容
17．（1）证明：正三角形内任一点（不与顶点重合）到三边的距离和为定值．（2）通过对（1）的类比，提出正四面体的一个正确的结论，并予以证明．
分析 （1）利用等面积，即可证明结论；
（2）根据平面中的某些性质类比推理出空间中的某些性质，一般遵循“点到线”，“线到面”，“面到体”等原则，由在平面几何中，已知“正三角形内一点到三边距离之和是一个定值”，是一个与线有关的性质，由此可以类比推出空间中一个与面有关的性质，再由割补法可证明结论．
解答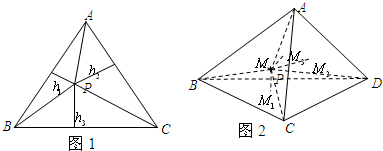 
（1）证明：图1所示，设P是正三角形ABC内任一点（不与顶点重合），
点P到正三角形三边的距离分别为h1，h2，h3，三角形边长为a，高为h，
则三角形的面积S=$\frac{1}{2}$ah=$\frac{1}{2}$ah1+$\frac{1}{2}$ah2+$\frac{1}{2}$ah3，------（4分）
即h=h1+h2+h3．
所以，正三角形内任一点（不与顶点重合）到三边的距离和为定值-------（5分）
（2）类比的结论是：正四面体内任一点（不与顶点重合）到它的四个面的距离和为定值．-------（8分）
下面给出证明：如图2：
设点P为正四面体ABCD内部任一点，且点P到四个面的距离分别为PM1，PM2，PM3，PM4，正四面体的高为h，
则点P将四面体分成四个共顶点的三棱锥．
因为ABCD为正四面体，所以四个面面积相同，
由VP-BCD+VP-ACD+VP-ABD+VP-ABC=VABCD得：PM1+PM2+PM3+PM4=h．-------（14分）
点评 本题考查的知识点是类比推理，类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7．下列有关命题说法正确的是（ ）
| A． | 命题“若x2=4，则x=2”的否命题为“若x2=4，则x≠2” | |
| B． | 所有常数列既是等差数列也是等比数列 | |
| C． | 命题“若x=y，则sinx=siny”的逆否命题为假命题 | |
| D． | 命题“?x∈R，x2+x＜0”的否定是“?x∈R，x2+x≥0”． |
设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E（如图），AE=EB=DE=2．现将△ADE沿DE折起，使二面角A-DE-B为90°，P，Q分别是线段AE和线段EB上任意一点，若MQ⊥PN时，求PQ长度的取值范围$[{\frac{{\sqrt{5}}}{5}，1}]$．
如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE．若M为线段A1C的中点，则在△ADE翻折过程中，下列命题正确的是①②④．（写出所有正确的命题的编号）