题目内容
15.能使不等式f(x)≤M成立的所有常数M中,我们把M的最小值叫做f(x)的上确界,若a>0,b>0且a+b=1,则$-\frac{1}{2a}-\frac{2}{b}$的上确界为( )| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
分析 根据题意和基本不等式求出$\frac{1}{2a}+\frac{2}{b}$的范围,再求出$-\frac{1}{2a}-\frac{2}{b}$的范围,由函数的上确界的定义即可求出答案.
解答 解:∵a>0,b>0且a+b=1,
∴$\frac{1}{2a}+\frac{2}{b}$=(a+b)($\frac{1}{2a}+\frac{2}{b}$)=$\frac{5}{2}+\frac{2a}{b}+\frac{b}{2a}$≥$\frac{5}{2}$+2$\sqrt{\frac{2a}{b}•\frac{b}{2a}}$=$\frac{9}{2}$,
当且仅当$\frac{2a}{b}=\frac{b}{2a}$取等号,
∴$-\frac{1}{2a}-\frac{2}{b}≤$-$\frac{9}{2}$,
由题意可得,$-\frac{1}{2a}-\frac{2}{b}$的上确界是$-\frac{9}{2}$,
故选:A.
点评 本题考查新定义的应用,基本不等式和“1”的代换,注意基本不等式的三个条件,属于基础题.

练习册系列答案
相关题目
10.已知直线l经过点P(3,4).
(1)若直线l的倾斜角为θ(θ≠90°),且直线l经过另外一点(cosθ,sinθ),求此时直线的方程;
(2)若直线l与两坐标轴围成等腰直角三角形,求直线l的方程.
(1)若直线l的倾斜角为θ(θ≠90°),且直线l经过另外一点(cosθ,sinθ),求此时直线的方程;
(2)若直线l与两坐标轴围成等腰直角三角形,求直线l的方程.
7.下列有关命题说法正确的是( )
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 所有常数列既是等差数列也是等比数列 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 命题“?x∈R,x2+x<0”的否定是“?x∈R,x2+x≥0”. |
4.已知点P(-3,4)在角α的终边上,则$\frac{sinα+cosα}{3sinα+2cosα}$的值为( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{18}$ | D. | -1 |
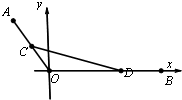 在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.
在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.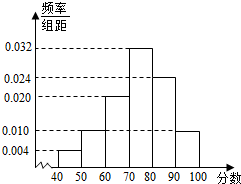 某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.