题目内容
已知函数 ,
,
(1)若 是常数,问当
是常数,问当 满足什么条件时,函数
满足什么条件时,函数 有最大值,并求出
有最大值,并求出 取最大值时
取最大值时 的值;
的值;
(2)是否存在实数对 同时满足条件:(甲)
同时满足条件:(甲) 取最大值时
取最大值时 的值与
的值与 取最小值的
取最小值的 值相同,(乙)
值相同,(乙) ?
?
(3)把满足条件(甲)的实数对 的集合记作A,设
的集合记作A,设 ,求使
,求使 的
的 的取值范围.
的取值范围.
(1) ,值域为
,值域为 ;(2)证明见解析;(3)存在,且
;(2)证明见解析;(3)存在,且 .
.
解析试题分析:(1)这是一个不等式恒成立问题,把不等式转化为 恒成立,那么这一定是二次不等式,恒成立的条件是
恒成立,那么这一定是二次不等式,恒成立的条件是 可解得
可解得 ,从而得到
,从而得到 的解析式,其值域也易求得;(2)要证明数列
的解析式,其值域也易求得;(2)要证明数列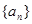 在该区间上是递增数列,即证
在该区间上是递增数列,即证 ,也即
,也即 ,根据
,根据 的定义,可把
的定义,可把 化为关于
化为关于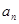 的二次函数,再利用
的二次函数,再利用 ,可得结论
,可得结论 ;(3)这是一道存在性问题,解决问题的方法一般是假设存在符合题意的结论,本题中假设
;(3)这是一道存在性问题,解决问题的方法一般是假设存在符合题意的结论,本题中假设 存在,使不等式成立,为了求出
存在,使不等式成立,为了求出 ,一般要把不等式左边的和求出来,这就要求我们要研究清楚第一项是什么?这个和是什么数列的和?由
,一般要把不等式左边的和求出来,这就要求我们要研究清楚第一项是什么?这个和是什么数列的和?由 ,从而
,从而 ,
,

 ,不妨设
,不妨设 ,则
,则 (
( ),对这个递推公式我们可以两边取对数把问题转化为
),对这个递推公式我们可以两边取对数把问题转化为 ,这是数列
,这是数列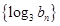 的递推公式,可以变为一个等比数列,方法是上式可变为
的递推公式,可以变为一个等比数列,方法是上式可变为 ,即数列
,即数列 是公比为2的等比数列,其通项公式易求,反过来,可求得
是公比为2的等比数列,其通项公式易求,反过来,可求得 ,从而求出不等式左边的和,化简不等式.
,从而求出不等式左边的和,化简不等式.
试题解析:(1)由 恒成立等价于
恒成立等价于 恒成立,
恒成立,
从而得: ,化简得
,化简得 ,从而得
,从而得 ,所以
,所以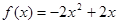 ,
,
3分
其值域为 . 4分
. 4分
(2)解: 
6分 , 8分
, 8分
从而得 ,即
,即 ,所以数列
,所以数列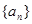 在区间
在区间 上是递增数列.
上是递增数列.
10分
(3)由(2)知 ,从而
,从而 ;
; ,即
,即 ;
;
12分
令 ,则有
,则有 且
且 ;
;
从而有 ,可得
,可得 ,所以数列
,所以数列 是
是 为首项,公比为
为首项,公比为 的等比数列,
的等比数列,
从而得 ,即
,即 ,
,
所以  ,
,
所以 ,所以
,所以 ,
,
所以,
 .
.
即

 ,所以,
,所以, 恒成立.
恒成立.
15分
当 为奇数时,即
为奇数时,即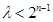 恒成立,当且仅当
恒成立,当且仅当 时,
时, 有最小值
有最小值 为.
为.
练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 .
. ,
, ,求使
,求使 恒成立的实数
恒成立的实数 的取值范围.
的取值范围. 的公比为q,且
的公比为q,且 ,
, 表示不超过实数
表示不超过实数 的最大整数(如
的最大整数(如 ),记
),记 ,数列
,数列 项和为
项和为 ,数列
,数列 的前
的前 .
. ,求
,求 ;
; (
( )的充分必要条件为
)的充分必要条件为 ;
; 的正整数n,都有
的正整数n,都有 ,证明:
,证明: .
. 满足
满足 ,且
,且 ,其中
,其中 .
. 满足
满足 是否存在正整数m、n(1<m<n),使得
是否存在正整数m、n(1<m<n),使得 成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。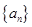 的前
的前 项和是
项和是 ,且
,且 .求数列
.求数列 的前n项和为
的前n项和为 ,
,
 是等比数列;
是等比数列; ,数列
,数列 的前n项和为
的前n项和为 ,求不超过
,求不超过 的最大整数的值.
的最大整数的值. 中,
中, ,设
,设 .
. 的前三项;
的前三项; ;
; 项和为
项和为 ,求证:
,求证: .
. 的各项均为正数,
的各项均为正数, ,
, .
. .证明:
.证明: 为等差数列,并求
为等差数列,并求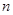 项和
项和 .
.