题目内容
已知各项均为正数的数列 满足
满足 ,且
,且 ,其中
,其中 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 满足
满足 是否存在正整数m、n(1<m<n),使得
是否存在正整数m、n(1<m<n),使得 成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
(Ⅰ)数列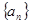 的通项公式为
的通项公式为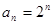
 ;(Ⅱ)存在,
;(Ⅱ)存在, ,
,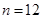 .
.
解析试题分析:(Ⅰ)求数列 的通项公式,首先须知道数列
的通项公式,首先须知道数列 的特征,由题意
的特征,由题意 可得,
可得,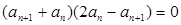 ,由于各项均为正数,故有
,由于各项均为正数,故有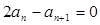 ?即
?即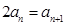 ,这样得到数列
,这样得到数列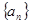 是公比为
是公比为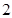 的等比数列,由
的等比数列,由 可求出
可求出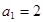 ,从而可得数列
,从而可得数列 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列 满足
满足 是否存在正整数
是否存在正整数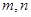
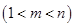 ,使得
,使得 成等比数列,首先求出数列
成等比数列,首先求出数列 的通项公式,
的通项公式,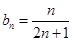 ,然后假设存在正整数
,然后假设存在正整数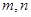
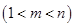 ,使得
,使得 成等比数列,则
成等比数列,则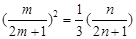 ,整理可得
,整理可得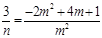 ,只要
,只要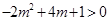 即可,解不等式求出
即可,解不等式求出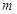 的范围,看是否有正整数,从而的结论.
的范围,看是否有正整数,从而的结论.
试题解析:(Ⅰ)??因为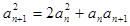 ?即
?即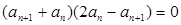 ?
?
又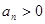 ?所以有
?所以有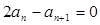 ?即
?即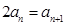
所以数列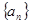 是公比为
是公比为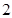 的等比数列?
的等比数列?
由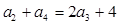 得
得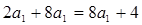 ?解得
?解得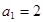 。
。
从而,数列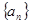 的通项公式为
的通项公式为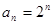
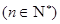 。 6分
。 6分
(II)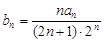 =
=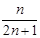 ,若
,若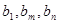 成等比数列,则
成等比数列,则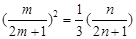 ,
,
即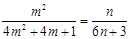 .
.
由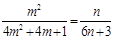 ,可得
,可得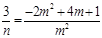 ,
,
所以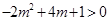 ,解得:
,解得: 。
。
又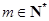 ,且
,且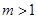 ,所以
,所以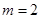 ,此时
,此时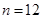 .
.
故当且仅当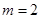 ,
,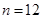 ?使得
?使得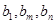 成等比数列。 13分
成等比数列。 13分
考点:等比数列的定义,及通项公式,探索性命题.

练习册系列答案
相关题目
 中,
中,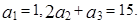
 通项公式;
通项公式; 满足
满足 ,求数列
,求数列 的前
的前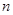 项和
项和 。
。 }的前n项和为
}的前n项和为 ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 项和
项和 ;
; ,
, .求不超过
.求不超过 的最大整数的值.
的最大整数的值. ,
,
 是常数,问当
是常数,问当 有最大值,并求出
有最大值,并求出 的值;
的值; 同时满足条件:(甲)
同时满足条件:(甲) 取最小值的
取最小值的 ?
? ,求使
,求使 的
的 的取值范围.
的取值范围. ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示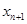 ;
; ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前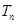 ,求
,求 的首项
的首项 ,公差
,公差 .且
.且 分别是等比数列
分别是等比数列 的
的 .
. 与
与 的通项公式;
的通项公式; 对任意自然数
对任意自然数 均有
均有
 成立,求
成立,求
 的值.
的值. 的前
的前 项和为
项和为 ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 .
.