题目内容
已知数列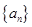 的前
的前 项和是
项和是 ,且
,且 .求数列
.求数列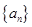 的通项公式;
的通项公式;
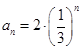
解析试题分析:由题意根据数列前 项和定义,尽可能对条件
项和定义,尽可能对条件 进行挖掘利用,因为
进行挖掘利用,因为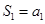 ,所以由条件可求出数列
,所以由条件可求出数列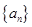 的首项
的首项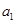 ,当
,当 时,有
时,有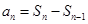 ,由条件可得
,由条件可得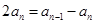 ,即
,即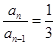 ,从而发现数列
,从而发现数列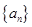 是以首项为
是以首项为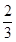 ,公比为
,公比为 的等比数列,再由等比数列的通项公式可求得数列
的等比数列,再由等比数列的通项公式可求得数列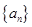 的通项公式.
的通项公式.
试题解析:当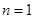 时,
时,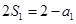 ,
,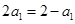 ,∴
,∴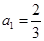 ; 2分
; 2分
当 时,
时,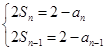 4分
4分
两式相减得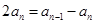 ,即
,即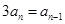 ,又
,又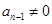 ,∴
,∴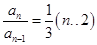 8分
8分
∴数列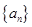 是以
是以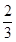 为首项,
为首项, 为公比的等比数列. 10分
为公比的等比数列. 10分
∴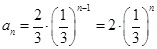 12分
12分
考点:1.数列前 项和定义;2.等比数列.
项和定义;2.等比数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, ,
,
 ,设
,设 .
. 是等比数列;
是等比数列; 的前
的前 项和
项和 ;
; ,
, 为数列
为数列 的前
的前 的最大的整数.
的最大的整数.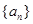 为等比数列,
为等比数列,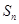 为其前
为其前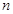 项和,已知
项和,已知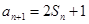 .
.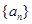 的通项公式;
的通项公式;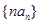 的前
的前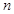 项和
项和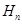 .
.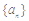 满足:
满足: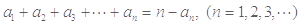
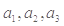 的值;
的值;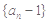 是等比数列;
是等比数列;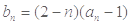 (
(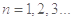 ),如果对任意
),如果对任意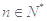 ,都有
,都有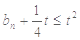 ,求实数
,求实数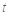 的取值范围.
的取值范围. ,
,
 是常数,问当
是常数,问当 有最大值,并求出
有最大值,并求出 的值;
的值; 同时满足条件:(甲)
同时满足条件:(甲) 取最小值的
取最小值的 ?
? ,求使
,求使 的
的 的取值范围.
的取值范围.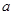 为实数,数列
为实数,数列 满足
满足 ,当
,当 时,
时, ,
,  ;(5分)
;(5分) ,使
,使 ;(5分)
;(5分) ,当
,当 时,求证:
时,求证: (6分)
(6分) 中,
中,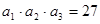 ,
,
 和公比
和公比 ;
; .
. 的首项
的首项 其中
其中 ,
, 令集合
令集合 .
. 是数列
是数列 ;
; 时,求集合
时,求集合 中元素个数
中元素个数 的最大值.
的最大值.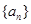 为等比数列, 其前
为等比数列, 其前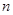 项和为
项和为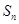 , 已知
, 已知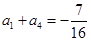 , 且对于任意的
, 且对于任意的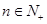 有
有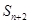 ,
, 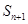 成等差;求数列
成等差;求数列