题目内容
4.设f(x)=sin(2x+φ)(-π<φ<0),y=f(x)的一条对称轴为直线x=$\frac{π}{8}$.(1)求φ;
(2)求单调区间;
(3)求f(x)在[0,$\frac{π}{2}$)上的最值;
(4)如何将sinx图象变换成y=f(x)的图象.
分析 (1)由条件利用正弦函数的图象的对称性求得φ的值.
(2)由条件利用正弦函数的单调性求出函数f(x)的增区间和减区间.
(3)由条件利用正弦函数的定义域、值域,求得f(x)在[0,$\frac{π}{2}$)上的最值.
(4)由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:(1)由题意可得2×$\frac{π}{8}$+φ=kπ+$\frac{π}{2}$,k∈z,求得 φ=kπ+$\frac{π}{4}$,k∈z.
再结合-π<φ<0,可得φ=-$\frac{3π}{4}$.
(2)由(1)可得f(x)=sin(2x-$\frac{3π}{4}$),令2kπ-$\frac{π}{2}$≤2x-$\frac{3π}{4}$≤2kπ+$\frac{π}{2}$,求得kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,k∈z,
可得函数的增区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈z.
令2kπ+$\frac{π}{2}$≤2x-$\frac{3π}{4}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{5π}{8}$≤x≤kπ+$\frac{8π}{8}$,k∈z,
可得函数的减区间为[kπ+$\frac{5π}{8}$,kπ+$\frac{9π}{8}$],k∈z.
(3)在[0,$\frac{π}{2}$)上,2x-$\frac{3π}{4}$∈[-$\frac{3π}{4}$,$\frac{π}{4}$),故当2x-$\frac{3π}{4}$=-$\frac{π}{2}$时,f(x)=sin( 2x-$\frac{3π}{4}$)取得最小值为-1;
当2x-$\frac{3π}{4}$趋于$\frac{π}{4}$时,f(x)=sin( 2x-$\frac{3π}{4}$)趋于最大值$\frac{\sqrt{2}}{2}$.
(4)把y=sinx的图象向右平移$\frac{3π}{4}$个单位,可得y=sin(x-$\frac{3π}{4}$)的图象;
再把所得图象上点的横坐标变为原来的$\frac{1}{2}$倍,可得f(x)=sin(2x-$\frac{3π}{4}$)的图象.
点评 本题主要考查正弦函数的图象的对称性,正弦函数的单调性,正弦函数的定义域和值域,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

 名校课堂系列答案
名校课堂系列答案| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
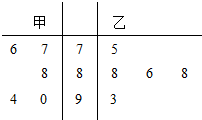 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )| A. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,乙比甲成绩稳定 | B. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,甲比乙成绩稳定 | ||
| C. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,乙比甲成绩稳定 |
| A. | $\frac{2\sqrt{34}}{17}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{4\sqrt{7}}{7}$ | D. | $\frac{4}{5}$ |

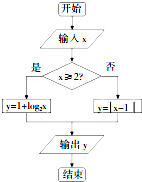 如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).
如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).