题目内容
19.函数y=$\sqrt{2{x}^{2}(1-2{x}^{2})}$的最大值为$\frac{1}{2}$.分析 由条件利用基本不等式,求得函数y=$\sqrt{2{x}^{2}(1-2{x}^{2})}$的最大值.
解答 解:函数y=$\sqrt{2{x}^{2}(1-2{x}^{2})}$≤$\frac{{2x}^{2}+(1-{2x}^{2})}{2}$=$\frac{1}{2}$,当且仅当2x2=1-2x2,即 x2=$\frac{1}{4}$时,取等号,
故函数y=$\sqrt{2{x}^{2}(1-2{x}^{2})}$的最大值为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查基本不等式的应用,注意检验等号成立条件是否具备,属于基础题.

练习册系列答案
相关题目
7.若命题“p或q”和命题“非p”均为真命题,则下列说法正确的是( )
| A. | p真q真 | B. | p真q假 | C. | p假q假 | D. | p假q真 |
4.若复数z满足z=$\frac{2i}{1-i}$,则在复平面内,z对应的点坐标是( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
8.已知x>0,y>0,且2x+y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值是( )
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
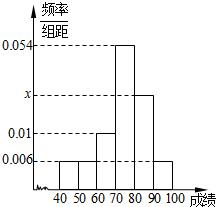 某班50位学生期中考试数学成绩的频率分布直方图如图所示.
某班50位学生期中考试数学成绩的频率分布直方图如图所示.