题目内容
【题目】已知不等式（ax+2）ln（x+a）≤0对x∈（﹣a，+∞）恒成立，则a的值为 ．
【答案】﹣1
【解析】解：∵x∈（﹣a，+∞），
∴当﹣a＜x＜1﹣a时，y=ln（x+a）＜0，
当x＞1﹣a时，y=ln（x+a）＞0，
又（ax+2）ln（x+a）≤0对x∈（﹣a，+∞）恒成立，①若a＞0，y=ax+2与y=ln（x+a）均为定义域上的增函数，
在x∈（﹣a，+∞）上，可均大于0，不满足题意；②若a=0，则2lnx）≤0对x∈（0，+∞）不恒成立，不满足题意；
∴a＜0．
作图如下：
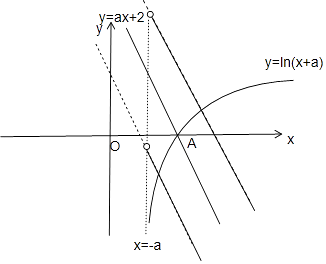
由图可知，当且仅当方程为y=ln（x+a）的曲线与方程为y=ax+2的直线相交于点A，
即满足 
时，（ax+2）ln（x+a）≤0对x∈（﹣a，+∞）恒成立，
解方程 得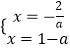 
，解得a=﹣1．
所以答案是：﹣1．
练习册系列答案
相关题目
