题目内容
【题目】已知点P(x,y)在圆x2+y2﹣6x﹣6y+14=0上
(1)求 ![]() 的最大值和最小值;
的最大值和最小值;
(2)求x2+y2+2x+3的最大值与最小值;
(3)求x+y的最大值与最小值.
【答案】
(1)解:如图示:
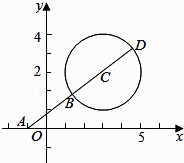 ,
,
圆x2+y2﹣6x﹣6y+14=0即为(x﹣3)2+(y﹣3)2=4,
可得圆心为C(3,3),半径为r=2,
设k= ![]() ,即kx﹣y=0,
,即kx﹣y=0,
则圆心到直线的距离d≤r,
即 ![]() ≤2,
≤2,
平方得5k2﹣18k+5≤0,
解得: ![]() ≤k≤
≤k≤ ![]() ,
,
故 ![]() 的最大值是
的最大值是 ![]() ,最小值为
,最小值为 ![]()
(2)解:x2+y2+2x+3=(x+1)2+y2+2
表示点(x,y)与A(﹣1,0)的距离的平方加上2,
连接AC,交圆C于B,延长AC,交圆于D,
可得AB为最短,且为|AC|﹣r= ![]() ﹣2=3,
﹣2=3,
AD为最长,且为|AC|+r=5+2=7,
则x2+y2+2x+3 的最大值为72+2=51,
x2+y2+2x+3的最小值为32+2=11
(3)解:圆x2+y2﹣6x﹣6y+14=0即为(x﹣3)2+(y﹣3)2=4,
令x﹣3=2cosa,y﹣3=2sina,
则x+y=6+2(cosa+sina)=6+2 ![]() sin(a+
sin(a+ ![]() ),
),
∵﹣1≤sin(a+ ![]() )≤1,
)≤1,
∴6﹣2 ![]() ≤6+2
≤6+2 ![]() sin(a+
sin(a+ ![]() )≤6+2
)≤6+2 ![]() ,
,
∴x+y的最大值为6+2 ![]() ,最小值为6﹣2
,最小值为6﹣2 ![]()
【解析】(1)求得已知圆的圆心和半径,设k= ![]() ,即kx﹣y=0,则圆心到直线的距离d≤r,加上即可得到最值;(2)x2+y2+2x+3=(x+1)2+y2+2表示点(x,y)与A(﹣1,0)的距离的平方加上2,连接AC,交圆C于B,延长AC,交圆于D,可得AB最短,AD最长,加上即可得到所求最值;(3)化简可得(x﹣3)2+(y﹣3)2=4,从而令x﹣3=2cosa,y﹣3=2sina,从而利用三角函数求最值.
,即kx﹣y=0,则圆心到直线的距离d≤r,加上即可得到最值;(2)x2+y2+2x+3=(x+1)2+y2+2表示点(x,y)与A(﹣1,0)的距离的平方加上2,连接AC,交圆C于B,延长AC,交圆于D,可得AB最短,AD最长,加上即可得到所求最值;(3)化简可得(x﹣3)2+(y﹣3)2=4,从而令x﹣3=2cosa,y﹣3=2sina,从而利用三角函数求最值.
